题目内容
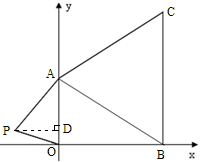
如图在下面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式: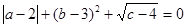
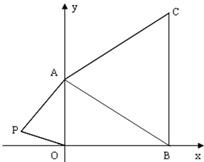
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,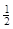 ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△AOP的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
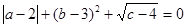

(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,
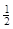 ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△AOP的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
(1)a=2,b=3,c=4;(2)3-m;(3)存在,P(-3,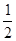 )
)
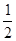 )
)试题分析:(1)根据非负数的性质:若几个非负数的和为0,这几个数均为0,即可求得结果;
(2)过点p作PD⊥y轴于点D,由
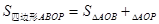 根据三角形的面积公式求解即可;
根据三角形的面积公式求解即可;(3)由
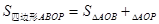 可得
可得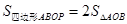 ,即可得到关于m的方程,再解出即可.
,即可得到关于m的方程,再解出即可.解:(1)因为
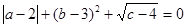 ,
,所以a=2,b=3,c=4;
(2)过点p作PD⊥y轴于点D
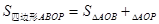 =
=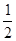 ×2×3+
×2×3+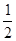 ×2×(-m)=3-m;
×2×(-m)=3-m;(3)存在点P使四边形ABOP的面积为△AOP的面积的两倍
因为
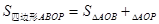
所以
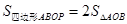 ,即3-m=2×(
,即3-m=2×(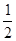 ×2×3),解得m=-3
×2×3),解得m=-3所以P(-3,
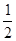 ).
).点评:此类问题知识点多,综合性强,难度较大,一般是中考压轴题,需仔细分析.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目



 .已知∠AOB=30°,∠B=90°,AB=1,则
.已知∠AOB=30°,∠B=90°,AB=1,则 点的坐标为( ).
点的坐标为( ).



