题目内容
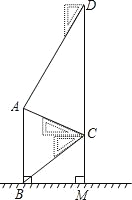
【题目】如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:![]() ≈1.73).
≈1.73).
【答案】雕塑AB的高度约为6.6米.
【解析】
试题分析:首先过点C作CE⊥AB于E,然后利用三角函数的性质,求得CD,AC的长,然后在Rt△ACE中,求得AE的长,继而求得CE的长,又在Rt△BCE中,求得BE的长,继而求得答案.
试题解析:过点C作CE⊥AB于E.

∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=9.6,
∴AC=![]() CD=4.8.
CD=4.8.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴AE=![]() AC=2.4,
AC=2.4,
CE=ACcos∠ACE=4.8cos30°=![]() .
.
在Rt△BCE中,∵∠BCE=45°,
∴BE=CE=![]() ,
,
∴AB=AE+BE=2.4+![]() ≈6.6(米).
≈6.6(米).
答:雕塑AB的高度约为6.6米.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目