题目内容
【题目】如图，把△ABC纸片沿MN折叠，使点C落在四边形ABNM的内部时，则∠1、∠2和 ∠C之间有一种数量关系始终保持不变. 这个关系是___.
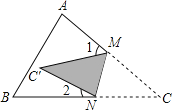
【答案】2∠C=∠1+∠2
【解析】
根据三角形内角和定理得出∠C′=180°-∠C′MN-∠C′NM，再由图形翻折变换的性质即可得出结论．
解：在△C′MN中，
∵∠C′+∠C′MN+∠C′NM=180°，
∴∠C′=180°-∠C′MN-∠C′NM，
由折叠的性质得：∠1+2∠C′MN=180°，∠2+2∠C′NM=180°，
∴∠1+2∠C′MN+∠2+2∠C′NM=360°，∠C=∠C′，
∴∠1+∠2=360°-2∠C′MN-2∠C′NM=2（180°-∠C′MN-∠C′NM）=2∠C′，
∴2∠C=∠1+∠2．
故答案为：2∠C=∠1+∠2．
练习册系列答案
新思维寒假作业系列答案
相关题目
【题目】一张长方形桌子可坐6人，按下图方式讲桌子拼在一起．
………
① ② ③
（1）观察图形，填写下表：
图形（n） | ② | ③ | …… | n |
坐的人数（人） | …… |
（2）一家餐厅有40张这样的长方形桌子，按照上图的方式每5张拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？
（3）在（2）中，若改为每8张桌子拼成1张大桌子，则共可坐多少人？
