题目内容
【题目】若二次函数y=（k﹣2）x2+（2k+1）x+k的图象与x轴有两个交点，其中只有一个交点落在﹣1和0之间（不包括﹣1和0），那么k的取值范围是 ．
【答案】0＜k＜2
【解析】解：如图1，当k﹣2＞0，即k＞2时，抛物线开口向上，
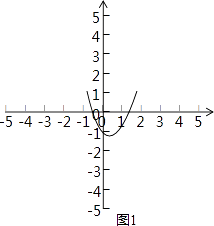
∵只有一个交点落在﹣1和0之间，
∴当x=﹣1时，y＞0，当x=0时，y＜0，
∴ 
，
解得k＜0，
不合题意；
如图2，当k﹣2＜0，即k＜2时，抛物线开口向下，
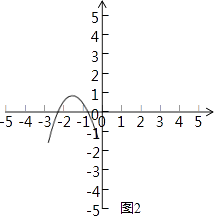
∵只有一个交点落在﹣1和0之间，
∴当x=﹣1时，y＜0，当x=0时，y＞0，
，
解得，k＞0，
∴0＜k＜2，
∴k的取值范围是0＜k＜2．
【考点精析】根据题目的已知条件，利用抛物线与坐标轴的交点的相关知识可以得到问题的答案，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
