题目内容
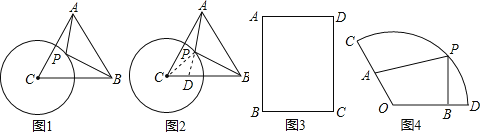
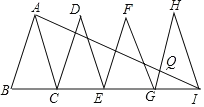
【题目】如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交GH于点Q.
(1)求证:△IAB∽△ACB;
(2)求HQ:QG的值.
【答案】(1)证明见解析;(2)HQ:QG=3.
【解析】
(1)由题意得出BC=1,BI=4,则![]() 再由∠ABI=∠ABC,得△IAB∽△ACB;
再由∠ABI=∠ABC,得△IAB∽△ACB;
(2)由GQ∥AB可得![]() ,求出
,求出![]() ,则
,则![]() ,则HQ:QG的值可求出.
,则HQ:QG的值可求出.
(1)∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴HI=AB=2,GI=BC=1,BI=4BC=4,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠ABI=∠ABC,
∴△IAB∽△ACB;
(2)∵∠ABC=∠HGI,
∴GQ∥AB,
∴△QGI∽△ABI,
∴![]() ,
,
∴QG![]() ,
,
∴QH=2![]() ,
,
∴HQ:QG=3.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
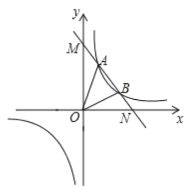
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点A(
的图象交于点A(![]() )、
)、![]() 两点,与坐标轴分别交于M、N两点.
两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 中
中![]() 的取值范围是____________;
的取值范围是____________;
(3)求△ABC的面积.