��Ŀ����
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,A(8,6),C(0,10)��AC=CO��ֱ��AC��x���ڵ�M������AOC��ֱ��AC���ۣ�ʹ�õ�O���ڵ�B��������AB��x����D������P�ӵ�O��������2����λ����/����ٶ�������OA�˶���ͬʱ����Q��A������ÿ��1����λ���ٶ�������AB�˶���

(1)��B������ꣻ
(2)����PB�����P���˶�ʱ��Ϊt�룬��PAB�����ΪS����S��t�Ĺ�ϵʽ����ֱ��дt��ȡֵ��Χ��
(3)�ڵ�P��Q�˶������У���tΪ��ֵʱ����APQ����PQΪ�ױߵĵ���������?��ֱ��д��Q�����ꡣ
���𰸡���1����8��-4������2��s=16t+80��0t5����3��t=![]() ��(8,
��(8, ![]() )
)
.
��������
��1�����ݷ��۵����ʣ��ɵ�OA=AB��OC=BC���������ε��ж������ʣ��ɵ�![]() ��
��
��2�����ݹ��ɶ������ɵ�OB��AC�ij����������ε�������ɵ�BE�ij������������ε������ʽ���ɵú�����ϵʽ��
����OP��OA�Ĺ�ϵ���ɵ��Ա�����ȡֵ��Χ��
��3�������߶εĺͲ�ɵ�AP�����ݵ��������εĶ��壬�ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣�
(1)����AOC��ֱ��AC���ۣ�ʹ�õ�O���ڵ�B������
OA=AB��OC=BC.
��AC=CO=10����
AO=CO=CB=BA=10.
�ı���AOCB�����Σ�
![]() ,��x
,��x![]() =8��
=8��
![]() ,��y
,��y![]() =610=4��
=610=4��
��B������(8,4)��
(2)��ͼ��BE��OA��E��
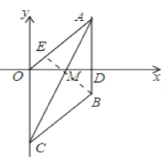
�ɹ��ɶ�������
OB=![]() ,AC=
,AC=![]() =8
=8![]() ��
��
������������
OABE=ACOB��
��BE=4![]() ��8
��8![]() ��10=16��
��10=16��
OP=2t��AP=102t��
S��ABP=![]() APBE=
APBE=![]() (102t)��16=16t+80��
(102t)��16=16t+80��
S��t�Ĺ�ϵʽΪs=16t+80��
��OPAO����2t10�����t5��
��ʱ���ǷǸ�������t0��
�Ա�����ȡֵ��Χ��0t5��
(3)��OP=2t����AP=OAOP=102t.
AQ=t.
��AP=AQ����
102t=t.
���t=![]() ��
��
��t=![]() ʱ����APQ����PQΪ�ױߵĵ��������Σ�
ʱ����APQ����PQΪ�ױߵĵ��������Σ�
��AB��y�ᣬ��
Q��ĺ�����Ϊ8,������Ϊ6![]() =
=![]() ��
��
��Q�������Ϊ(8, ![]() )
)







