题目内容
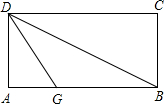 折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠AD边与对角线BD重叠,得折痕DG,若AB=2 BC=1,则AG的长为
折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠AD边与对角线BD重叠,得折痕DG,若AB=2 BC=1,则AG的长为
- A.3-

- B.3+

- C.
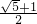
- D.
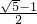
D
分析:首先设A与E重合,连接EG,由四边形ABCD是矩形,根据勾股定理,即可求得BD的长,又由折叠的性质,设AG=x,则GE=AG=x,在直角△BGE中,由勾股定理即可得到方程:( -1)2+x2=(2-x)2,解此方程即可求得AG的长.
-1)2+x2=(2-x)2,解此方程即可求得AG的长.
解答: 解:设A与E重合,连接EG,
解:设A与E重合,连接EG,
∵四边形ABCD是矩形,
∴AD=BC=DE=1,∠BAD=90°,
在直角△ABD中,BD=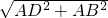 =
=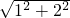 =
= ,
,
设AG=x,则GE=AG=x.
在直角△BGE中,BE=BD-DE= -1,BG=2-x.
-1,BG=2-x.
根据勾股定理可得:( -1)2+x2=(2-x)2,
-1)2+x2=(2-x)2,
解得:x=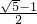 .
.
∴AG=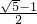 .
.
故选D.
点评:本题考查了矩形的性质,勾股定理,以及折叠的性质.注意正确利用线段长度之间的关系转化成方程问题是关键.
分析:首先设A与E重合,连接EG,由四边形ABCD是矩形,根据勾股定理,即可求得BD的长,又由折叠的性质,设AG=x,则GE=AG=x,在直角△BGE中,由勾股定理即可得到方程:(
 -1)2+x2=(2-x)2,解此方程即可求得AG的长.
-1)2+x2=(2-x)2,解此方程即可求得AG的长.解答:
 解:设A与E重合,连接EG,
解:设A与E重合,连接EG,∵四边形ABCD是矩形,
∴AD=BC=DE=1,∠BAD=90°,
在直角△ABD中,BD=
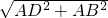 =
=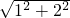 =
= ,
,设AG=x,则GE=AG=x.
在直角△BGE中,BE=BD-DE=
 -1,BG=2-x.
-1,BG=2-x.根据勾股定理可得:(
 -1)2+x2=(2-x)2,
-1)2+x2=(2-x)2,解得:x=
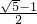 .
.∴AG=
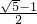 .
.故选D.
点评:本题考查了矩形的性质,勾股定理,以及折叠的性质.注意正确利用线段长度之间的关系转化成方程问题是关键.

练习册系列答案
相关题目
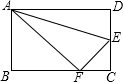 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
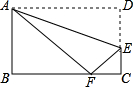 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则tan∠EFC的值为
如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处,已知AB=8,BC=10,则tan∠EFC的值为 折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠AD边与对角线BD重叠,得折痕DG,若AB=2 BC=1,则AG的长为( )
折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠AD边与对角线BD重叠,得折痕DG,若AB=2 BC=1,则AG的长为( ) 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,则AG的长是
如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,则AG的长是 如图,折叠矩形纸片ABCD,先折出对角线BD,再折叠,使AD边与BD重合,得到折痕DG,若AB=8,BC=6,求AG的长.
如图,折叠矩形纸片ABCD,先折出对角线BD,再折叠,使AD边与BD重合,得到折痕DG,若AB=8,BC=6,求AG的长.