题目内容
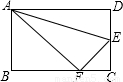
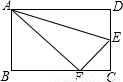
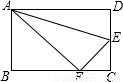
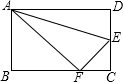
如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处，已知AB=8，BC=10，则tan∠EFC的值为分析：根据折叠的性质和锐角三角函数的概念来解决．
解答：解：根据题意可得：在Rt△ABF中，有AB=8，AF=AD=10，BF=6，
由同角的余角相等，可得∠BAF=∠CFE，
又因为∠B=∠C，
则Rt△ABF∽Rt△EFC，
故有∠EFC=∠BAF，
故tan∠EFC=tan∠BAF=
=
．
故答案为：
．
由同角的余角相等，可得∠BAF=∠CFE，
又因为∠B=∠C，
则Rt△ABF∽Rt△EFC，
故有∠EFC=∠BAF，
故tan∠EFC=tan∠BAF=
| 6 |
| 8 |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查锐角三角函数的概念：在直角三角形中，正弦等于对比斜；余弦等于邻比斜；正切等于对比邻．
练习册系列答案
相关题目
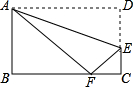
如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处已知AB=8，BC=10，则tan∠EFC的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
