题目内容

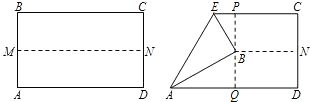
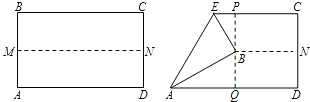
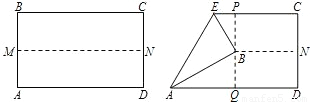
如图，先把矩形ABCD对折，折痕为MN，再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B'，则∠EAB'=


  1. A.
    15°
  2. B.
    30°
  3. C.
    45°
  4. D.
    60°
B
分析：利用等腰三角形三线合一可得∠EAB′=∠FAB′，由折叠可得∠EAB′=∠BAE，那么组成直角的三个角相等，每个角都为30°．
解答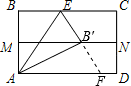：解：延长EB′交于AD于点F，由于MA是矩形的中位线，则点B′是EF的中点，所以AE=AF，
∴∠EAB′=∠FAB′=∠BAE=∠BAD=30°，故选B．
点评：本题利用了：1、折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；
2、线段垂直平分线上的点与这条线段两个端点的距离相等及等腰三角形三线合一性质．
练习册系列答案
相关题目
小明想把一个三角形拼接成面积与它相等的矩形．他先进行了如下部分操作，如图1所示：作△ABC的中位线DE，过点A作AF⊥DE于点F，这样△ABC就被分成三部分．
（1）请你在图1中继续操作，把△ABC拼接成面积与它相等的矩形．（画出示意图）
（2）若把一个三角形通过类似的操作可以拼接成一个与原三角形面积相等的正方形，那么原三角形的一边a与这边上的高h之间的数量关系是
1：2
1：2
．
（3）在图2的网格中画出一个符合（2）中条件的三角形，并将其拼接成面积与它相等的正方形．（画出示意图）
根据所给的基本材料，请你进行适当的处理，编写一道综合题．
编写要求：①提出具有综合性、连续性的三个问题；②给出正确的解答过程；③写出编写意图和学生答题情况的预测．
材料①：如图，先把一矩形纸片ABCD对折，得到折痕MN，然后把B点叠在折痕线上，得到△ABE，再过点B把矩形ABCD第三次折叠，使点D落在直线AD上，得到折痕PQ．当沿着BE第四次将该纸片折叠后，点A就会落在EC上．
精英家教网
材料②：已知AC是∠MAN的平分线．
（1）在图1中，若∠MAN=120°，∠ABC=ADC=90°，求证：AB+AD=AC；
（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）在图3中：若∠MAN=α（0°＜α＜180°），∠ABC+∠ADC=180°，
则AB+AD=
 
AC（用含α的三角函数表示）．
精英家教网
材料③：
已知：如图甲，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿线段BA向点A匀速运动，速度为1cm/s；点Q由A出发沿线段AC向点C匀速运动，速度为2cm/s；连接PQ，设运动的时间为t（s）（0＜t＜2）．
精英家教网
编写试题选取的材料是
 
（填写材料的序号）
编写的试题是：（1）设△AQP的面积为y（cm2），求y与t之间的函数关系式．
（2）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值．
（3）如图（2），连接PC，并把△PQC沿QC翻折得到四边形PQP'C．是否存在某一时刻t，使四边形PQP'C为菱形？若存在，求出此时菱形的边长．
试题解答（写出主要步骤即可）：（1）过点Q作QD⊥AP于点D，证△AQD∽△ABC，利用相似性质及面积解答；
（2）分别求得Rt△ACB的周长和面积，由周长求出t，代入函数解析式验证；
（3）利用余弦定理得出PC、PQ，联立方程，求得t，再代入PC解得答案．

小明想把一个三角形拼接成面积与它相等的矩形．

他先进行了如下部分操作，如图所示：

①取△ABC的边AB、AC的中点D、E，联结DE；

②过点A作AF⊥DE于点F；

(1)请你帮小明完成上图的操作，把△ABC拼接成面积与它相等的矩形．

(2)若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形，那么原三角形的一边与这边上的高之间的数量关系是________．

(3)在下面所给的网格中画出符合(2)中条件的三角形，并将其拼接成面积与它相等的正方形．

根据所给的基本材料，请你进行适当的处理，编写一道综合题．
编写要求：①提出具有综合性、连续性的三个问题；②给出正确的解答过程；③写出编写意图和学生答题情况的预测．
材料①：如图，先把一矩形纸片ABCD对折，得到折痕MN，然后把B点叠在折痕线上，得到△ABE，再过点B把矩形ABCD第三次折叠，使点D落在直线AD上，得到折痕PQ．当沿着BE第四次将该纸片折叠后，点A就会落在EC上．

材料②：已知AC是∠MAN的平分线．
（1）在图1中，若∠MAN=120°，∠ABC=ADC=90°，求证：AB+AD=AC；
（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）在图3中：若∠MAN=α（0°＜α＜180°），∠ABC+∠ADC=180°，
则AB+AD=______AC（用含α的三角函数表示）．

材料③：
已知：如图甲，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿线段BA向点A匀速运动，速度为1cm/s；点Q由A出发沿线段AC向点C匀速运动，速度为2cm/s；连接PQ，设运动的时间为t（s）（0＜t＜2）．

编写试题选取的材料是______（填写材料的序号）
编写的试题是：（1）设△AQP的面积为y（cm2），求y与t之间的函数关系式．
（2）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值．
（3）如图（2），连接PC，并把△PQC沿QC翻折得到四边形PQP'C．是否存在某一时刻t，使四边形PQP'C为菱形？若存在，求出此时菱形的边长．
试题解答（写出主要步骤即可）：（1）过点Q作QD⊥AP于点D，证△AQD∽△ABC，利用相似性质及面积解答；
（2）分别求得Rt△ACB的周长和面积，由周长求出t，代入函数解析式验证；
（3）利用余弦定理得出PC、PQ，联立方程，求得t，再代入PC解得答案．
根据所给的基本材料，请你进行适当的处理，编写一道综合题．
编写要求：①提出具有综合性、连续性的三个问题；②给出正确的解答过程；③写出编写意图和学生答题情况的预测．
材料①：如图，先把一矩形纸片ABCD对折，得到折痕MN，然后把B点叠在折痕线上，得到△ABE，再过点B把矩形ABCD第三次折叠，使点D落在直线AD上，得到折痕PQ．当沿着BE第四次将该纸片折叠后，点A就会落在EC上．

材料②：已知AC是∠MAN的平分线．
（1）在图1中，若∠MAN=120°，∠ABC=ADC=90°，求证：AB+AD=AC；
（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）在图3中：若∠MAN=α（0°＜α＜180°），∠ABC+∠ADC=180°，
则AB+AD=______AC（用含α的三角函数表示）．

材料③：
已知：如图甲，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿线段BA向点A匀速运动，速度为1cm/s；点Q由A出发沿线段AC向点C匀速运动，速度为2cm/s；连接PQ，设运动的时间为t（s）（0＜t＜2）．

编写试题选取的材料是______（填写材料的序号）
编写的试题是：（1）设△AQP的面积为y（cm2），求y与t之间的函数关系式．
（2）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值．
（3）如图（2），连接PC，并把△PQC沿QC翻折得到四边形PQP'C．是否存在某一时刻t，使四边形PQP'C为菱形？若存在，求出此时菱形的边长．
试题解答（写出主要步骤即可）：（1）过点Q作QD⊥AP于点D，证△AQD∽△ABC，利用相似性质及面积解答；
（2）分别求得Rt△ACB的周长和面积，由周长求出t，代入函数解析式验证；
（3）利用余弦定理得出PC、PQ，联立方程，求得t，再代入PC解得答案．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网