题目内容
【题目】我们把经过原点,顶点落在同一抛物线C上的所有抛物线称为抛物线C的派生抛物线.
(1)若y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,求a的值.
(2)证明:经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:y=![]() x2+
x2+![]() 的派生抛物线;
的派生抛物线;
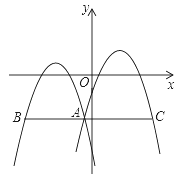
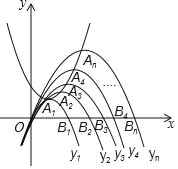
(3)如图,抛物线y1,y2,y3,y4…yn都是抛物线C:y=x2﹣2x+2的派生抛物线,其顶点A1,A2,A3,A4…An的横坐标分别是1、2、3、4…n,它们与x轴的另一个交点分别是B1,B2,B3,B4…Bn,与原点O构成的三角形分别为△OA1B1,△OA2B2,△OA3B3,△OA4B4…△OAnBn.
①请用含n的代数式表示抛物线yn的函数表达式;
②在这些三角形中,是否存在两个相似的三角形,若存在,请直接写出它们所对应的两个函数的表达式,若不存在,请说明理由.
【答案】(1)a=![]() ;(2)见解析;(3)①yn=﹣
;(2)见解析;(3)①yn=﹣![]() (x﹣n)2+n2﹣2n+2,②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,理由见解析.
(x﹣n)2+n2﹣2n+2,②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,理由见解析.
【解析】
(1)根据派生抛物线的定义构建方程求出a即可;
(2)根据派生抛物线的定义证明即可;
(3)①设yn=a(x-n)2+n2-2n+2,因为经过原点,可得0=a(0-n)2+n2-2n+2,推出a=![]()
②存在.y1=-(x-1)2+1,y2=-(x-2)2+2,理由:△OA1B1,△OA2B2都是等腰直角三角形;
(1)y1=﹣x2+4x的顶点坐标(2,4),
∵y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,
∴4=4a+2,
∴![]()
(2)∵抛物线经过原点(0,0),
∴m﹣2=0,
∴m=2,
∴抛物线的解析式为y=﹣2x2+4x,顶点(1,2),
当x=1时,![]()
∴抛物线的解析式为y=﹣2x2+4x,顶点(1,2)在抛物线C:![]()
∴经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:![]()
(3)①设yn=a(x﹣n)2+n2﹣2n+2,
∵经过原点,
∴0=a(0﹣n)2+n2﹣2n+2,
∴a=![]()
∴yn=﹣![]()
②存在.y1=﹣(x﹣1)2+1,y2=﹣(x﹣2)2+2,
理由:△OA1B1,△OA2B2都是等腰直角三角形.
∴△OA1B1∽△OA2B2.