题目内容
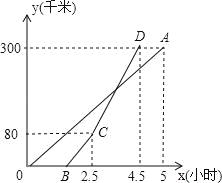
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
【答案】(1)30千米;(2)y=110x﹣195(2.5≤x≤4.5);(3)4.68小时.
【解析】
试题分析:(1)本题求出货车与轿车的速度是解题的关键.根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时,再根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米;(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解;(3)设货车从甲地出发x小时后再与轿车相遇,根据轿车(x﹣4.5)小时行驶的路程+货车x小时行驶的路程=300千米列出方程,解方程即可.
试题解析:(1)根据图象信息:货车的速度V货=![]() =60(千米/时).∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).轿车到达乙地后,货车距乙地30千米;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,∴
=60(千米/时).∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).轿车到达乙地后,货车距乙地30千米;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,∴![]() ,解得
,解得![]() ,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);(3)设货车从甲地出发后x小时后再与轿车相遇.∵V货车=60千米/时,所以V轿车=
,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);(3)设货车从甲地出发后x小时后再与轿车相遇.∵V货车=60千米/时,所以V轿车=![]() =110(千米/时),∴110(x﹣4.5)+60x=300,解得x≈4.68(小时).货车从甲地出发约4.68小时后再与轿车相遇.
=110(千米/时),∴110(x﹣4.5)+60x=300,解得x≈4.68(小时).货车从甲地出发约4.68小时后再与轿车相遇.

 阅读快车系列答案
阅读快车系列答案【题目】10袋小麦以每袋150千克为标准,超过150千克的部分记为正数,不足150千克的部分记为负数,记录情况如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
差值/kg | -6 | -3 | -1 | +7 | +3 | +4 | -3 | -2 | -2 | +1 |
(1)与标准重量相比较,10袋小麦总计超过或不足多少千克?
(2)每袋小麦的平均重量是多少千克?