题目内容
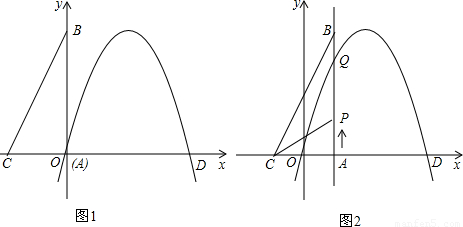
如图l,已知抛物线经过坐标原点O和x轴上另一点D,顶点的坐标为(2,4).直角三角形ABC的顶点A与点O重合,AC,AB分别在x轴,y轴上,且AC=3,AB=4.(1)直线BC的解析式为______;
(2)求该抛物线的函数关系式;
(3)将直角三角形ABC以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤2),AB边与该抛物线的交点为Q(如图2所示).
①设△CPQ的面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
②直接写出直线BC与抛物线有唯一的公共点时t的值.
【答案】分析:(1)首先求出B,C点坐标,再求直线BC的解析式;
(2)根据顶点式直接求出抛物线解析式即可;
(3)①根据题意得出P,Q点坐标,进而得出PQ的长,即可得出△CPQ的面积,再利用配方法得出最值;
②根据当直线BC与抛物线有唯一的公共点时,设此时直线解析式为:y= x+d,得出
x+d,得出 x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,
进而得出d的值,即可得出图象与x轴交点坐标,即可得出移动距离.
解答:解:(1)∵直角三角形ABC的顶点A与点O重合,AC,AB分别在x轴,y轴上,且AC=3,AB=4,
∴C,B坐标分别为:C(-3,0),B(0,4),
设BC直线解析式为:y=ax+b则:
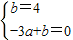 ,
,
解得: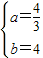 ,
,
∴y= x+4;
x+4;
故答案为:y= x+4;
x+4;
(2)∵抛物线的顶点坐标为(2,4),
∴设抛物线解析式为:y=a(x-2)2+4,
∵抛物线过原点,
∴0=4a+4,
解得:a=-1,
∴该抛物线的解析式为:y=-(x-2)2+4,即y=-x2+4x;
(3)①由题意得出点P的坐标为:(t,t),点Q的坐标为:(t,-t2+4t),
∴PQ=-t2+4t-t=-t2+3t,
∴△CPQ的面积为
S= PQ•AC
PQ•AC
= ×3×(-t2+3t)
×3×(-t2+3t)
=- (t2-3t)
(t2-3t)
=- (t-
(t- )2+
)2+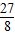
∴S存在最大值,最大值是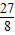 .
.
②当直线BC与抛物线有唯一的公共点时,
设此时直线解析式为:y= x+d,
x+d,
∴ x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,
∴b2-4ac=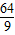 -4×1×d=0,
-4×1×d=0,
解得:d=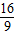 ,
,
∴此时BC所在直线解析式为:y= x+
x+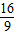 ,
,
∴y=0时,x=- ,
,
∴C点从(-3,0)到(- ,0)移动了
,0)移动了 个单位长度,
个单位长度,
∴直线BC与抛物线有唯一的公共点时t的值为: .
.
点评:此题主要考查了二次函数的综合应用以及配方法求最值以及根的判别式和待定系数法求一次函数解析式等知识,利用数形结合得出对应点位置是解题关键.
(2)根据顶点式直接求出抛物线解析式即可;
(3)①根据题意得出P,Q点坐标,进而得出PQ的长,即可得出△CPQ的面积,再利用配方法得出最值;
②根据当直线BC与抛物线有唯一的公共点时,设此时直线解析式为:y=
 x+d,得出
x+d,得出 x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,进而得出d的值,即可得出图象与x轴交点坐标,即可得出移动距离.
解答:解:(1)∵直角三角形ABC的顶点A与点O重合,AC,AB分别在x轴,y轴上,且AC=3,AB=4,
∴C,B坐标分别为:C(-3,0),B(0,4),
设BC直线解析式为:y=ax+b则:
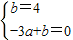 ,
,解得:
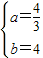 ,
,∴y=
 x+4;
x+4;故答案为:y=
 x+4;
x+4;(2)∵抛物线的顶点坐标为(2,4),
∴设抛物线解析式为:y=a(x-2)2+4,
∵抛物线过原点,
∴0=4a+4,
解得:a=-1,
∴该抛物线的解析式为:y=-(x-2)2+4,即y=-x2+4x;
(3)①由题意得出点P的坐标为:(t,t),点Q的坐标为:(t,-t2+4t),
∴PQ=-t2+4t-t=-t2+3t,
∴△CPQ的面积为
S=
 PQ•AC
PQ•AC=
 ×3×(-t2+3t)
×3×(-t2+3t)=-
 (t2-3t)
(t2-3t)=-
 (t-
(t- )2+
)2+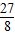
∴S存在最大值,最大值是
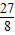 .
.②当直线BC与抛物线有唯一的公共点时,
设此时直线解析式为:y=
 x+d,
x+d,∴
 x+d=-x2+4x整理后方程为:x2-
x+d=-x2+4x整理后方程为:x2- x+d=0此时方程有两个相等的实数根,
x+d=0此时方程有两个相等的实数根,∴b2-4ac=
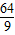 -4×1×d=0,
-4×1×d=0,解得:d=
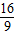 ,
,∴此时BC所在直线解析式为:y=
 x+
x+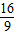 ,
,∴y=0时,x=-
 ,
,∴C点从(-3,0)到(-
 ,0)移动了
,0)移动了 个单位长度,
个单位长度,∴直线BC与抛物线有唯一的公共点时t的值为:
 .
.点评:此题主要考查了二次函数的综合应用以及配方法求最值以及根的判别式和待定系数法求一次函数解析式等知识,利用数形结合得出对应点位置是解题关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克. 探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=
探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC= 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克. 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经 ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.
