题目内容
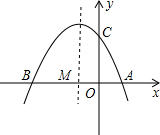 (2012•东莞模拟)如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点(1,0)和B(-3,0),与y轴交于C(0,3)
(2012•东莞模拟)如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点(1,0)和B(-3,0),与y轴交于C(0,3)(1)求抛物线的解析式,并求出顶点D的坐标.
(2)观察图象,直接写出一元二次不等式:ax2+bx+c<0解集为:
x>1或x<-3
x>1或x<-3
(3)若抛物线的对称轴交x轴于点M,求四边形BMCD的面积.
分析:(1)已知抛物线与y轴交于C(0,3),易知c=3,再把(1,0)、(-3,0)代入y=ax2+bx+3中,可得关于a、b的二元一次方程组,解即可求a、b,从而可得二次函数解析式;
(2)在点AB以外的x的取值都能使ax2+bx+c<0,即x>1或x<-3;
(3)观察可知S四边形BMCD=S△BDM+S△MCD,再根据三角形的面积公式可求其面积.
(2)在点AB以外的x的取值都能使ax2+bx+c<0,即x>1或x<-3;
(3)观察可知S四边形BMCD=S△BDM+S△MCD,再根据三角形的面积公式可求其面积.
解答: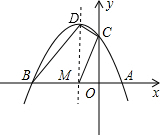 解:(1)∵抛物线与y轴交于C(0,3),
解:(1)∵抛物线与y轴交于C(0,3),
∴c=3,
∴y=ax2+bx+3,
把(1,0)、(-3,0)代入y=ax2+bx+3中,得
,
解得
,
∴二次函数的解析式是y=-x2-2x+3,
∴其顶点D的坐标是(-1,4);
(2)据图可知:ax2+bx+c<0解集为x>1或x<-3;
(3)S四边形BMCD=S△BDM+S△MCD=
×2×4+
×1×4=4+2=6.
 解:(1)∵抛物线与y轴交于C(0,3),
解:(1)∵抛物线与y轴交于C(0,3),∴c=3,
∴y=ax2+bx+3,
把(1,0)、(-3,0)代入y=ax2+bx+3中,得
|
解得
|
∴二次函数的解析式是y=-x2-2x+3,
∴其顶点D的坐标是(-1,4);
(2)据图可知:ax2+bx+c<0解集为x>1或x<-3;
(3)S四边形BMCD=S△BDM+S△MCD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了待定系数法求函数解析式、二次函数的性质、二次函数与不等式组,解题的关键是掌握解方程组,以及二次函数顶点的计算公式、三角形面积计算公式.

练习册系列答案
相关题目
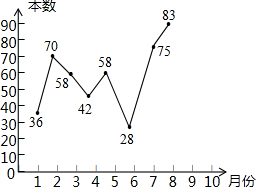 (2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
(2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )