题目内容
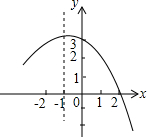 已知抛物线y=-
已知抛物线y=-| 3 | 8 |
(1)求b、c的值;
(2)求y的最大值;
(3)写出当y>0时,x的取值范围.
分析:(1)由抛物线对称轴为直线x=-1,利用对称轴公式列出关于b的方程,求出方程的解得到b的值,再由抛物线与y轴交于(0,3),可得出c的值为3;
(2)将(1)求出的b与c的值代入,确定出抛物线解析式,将解析式化为顶点形式,根据抛物线开口向下,有最大值,利用二次函数的性质即可求出y的最大值;
(3)令抛物线解析式中y=0,求出x的值,由抛物线开口向下,利用二次函数的图象可得出y大于0时x的范围.
(2)将(1)求出的b与c的值代入,确定出抛物线解析式,将解析式化为顶点形式,根据抛物线开口向下,有最大值,利用二次函数的性质即可求出y的最大值;
(3)令抛物线解析式中y=0,求出x的值,由抛物线开口向下,利用二次函数的图象可得出y大于0时x的范围.
解答:解:(1)由函数图象可得:抛物线的对称轴为直线x=-1,与y轴交于(0,3),
则-
=-1,解得b=
;
c=3;
(2)由(1)得到抛物线解析式为y=-
x2+
x+3=-
(x-1)2+
,
当x-1=0,即x=1时,y取得最大值,y最大值为
;
(3)令y=0,得到-
x2+
x+3=0,
整理得:x2-2x-8=0,即(x-4)(x+2)=0,
解得:x1=4,x2=-2,
故抛物线与x轴交于(4,0),(-2,0),
则当y>0时,x的取值范围-2<x<4.
则-
| b | ||
-2×
|
| 3 |
| 4 |
c=3;
(2)由(1)得到抛物线解析式为y=-
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 27 |
| 8 |
当x-1=0,即x=1时,y取得最大值,y最大值为
| 27 |
| 8 |
(3)令y=0,得到-
| 3 |
| 8 |
| 3 |
| 4 |
整理得:x2-2x-8=0,即(x-4)(x+2)=0,
解得:x1=4,x2=-2,
故抛物线与x轴交于(4,0),(-2,0),
则当y>0时,x的取值范围-2<x<4.
点评:此题考查了利用待定系数法确定二次函数解析式,以及二次函数的图象与性质,利用了数形结合的思想,数形结合思想是数学中重要的思想方法,学生做题时注意灵活运用.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目