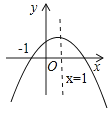题目内容
【题目】二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.-3
B.3
C.-6
D.9
【答案】B
【解析】(法1)∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0, ![]() ,即b2=12a,∵一元二次方程ax2+bx+m=0有实数根,
,即b2=12a,∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3,
∴m的最大值为3.
(法2)一元二次方程ax2+bx+m=0有实数根,
可以理解为y=ax2+bx和y=-m有交点,
可见,-m≥-3,∴m≤3,∴m的最大值为3.故选B.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目