题目内容
若直角三角形的面积为S，斜边长为c，则这个三角形的周长为
- A.
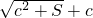
- B.
- C.
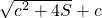
- D.
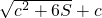
C
分析：设直角三角形两直角边长为a、b，利用勾股定理，三角形面积公式列出等式，再根据等式变形求a+b+c．
解答：设直角三角形两直角边长为a、b，
依题意，得ab=2S，a2+b2=c2，
则（a+b）2=a2+b2+2ab=c2+2S，
∵a、b为边长，a+b为正数，
∴a+b=
，
∴a+b+c=+c，
故选C．
点评：本题考查了利用勾股定理解直角三角形的能力，充分利用勾股定理，直角三角形的面积公式得出等式是解题的关键．
分析：设直角三角形两直角边长为a、b，利用勾股定理，三角形面积公式列出等式，再根据等式变形求a+b+c．
解答：设直角三角形两直角边长为a、b，
依题意，得ab=2S，a2+b2=c2，
则（a+b）2=a2+b2+2ab=c2+2S，
∵a、b为边长，a+b为正数，
∴a+b=
，∴a+b+c=
+c，故选C．
点评：本题考查了利用勾股定理解直角三角形的能力，充分利用勾股定理，直角三角形的面积公式得出等式是解题的关键．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
下列说法中，正确的个数有（ ）
①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为
；
②直角三角形的最大边长为
，最短边长为1，则另一边长为
；
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为
| 10 |
②直角三角形的最大边长为
| 3 |
| 2 |
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5．
| A、1个 | B、2个 | C、3个 | D、4个 |
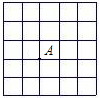如图，小正方形的边长为1，若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |