题目内容
如图,开口向下的抛物线y=ax2-8ax+12a与x轴交于A、B两点,抛物线上另有一点C在第一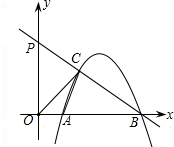 象限,且使△OCA∽△OBC,
象限,且使△OCA∽△OBC,(1)求OC的长及
| BC | AC |
(2)设直线BC与y轴交于P点,点C是BP的中点时,求直线BP和抛物线的解析式.
分析:(1)根据抛物线的解析式即可求出A、B的坐标,也就得出了OA、OB的长,根据题中给出的相似三角形得出的比例线段可求出OC的长.已知了OA、OB的长即可得出三角形OBC和三角形OCA的面积比,而根据面积比等于相似比的平方即可得出BC与AC的比例关系.
(2)当C是BP中点是,OC就是直角三角形OBP的斜边的中线,因此OC=BC,三角形OCB是等腰三角形,可过C作x轴的垂线通过构建直角三角形求出C点坐标,进而可得出直线BP的解析式,将C点坐标代入抛物线中即可求出二次函数的解析式.
(2)当C是BP中点是,OC就是直角三角形OBP的斜边的中线,因此OC=BC,三角形OCB是等腰三角形,可过C作x轴的垂线通过构建直角三角形求出C点坐标,进而可得出直线BP的解析式,将C点坐标代入抛物线中即可求出二次函数的解析式.
解答:解:
(1)由题设知a<0,
且方程ax2-8ax+12a=0有两二根,
两边同时除以a得,x2-8x+12=0
原式可化为(x-2)(x-6)=0
x1=2,x2=6
于是OA=2,OB=6
∵△OCA∽△OBC
∴OC2=OA•OB=12即OC=2
而
=
=
=
,故
=
(2)因为C是BP的中点
∴OC=BC从而C点的横坐标为3
又OC=2
∴C(3,
)
设直线BP的解析式为y=kx+b,
因其过点B(6,0),C(3,
),
则有
∴
∴y=-
x+2
又点C(3,
)在抛物线上
∴
=9a-24a+12a
∴a=-
∴抛物线解析式为:y=-
x2+
x-4
.
(1)由题设知a<0,
且方程ax2-8ax+12a=0有两二根,
两边同时除以a得,x2-8x+12=0
原式可化为(x-2)(x-6)=0
x1=2,x2=6
于是OA=2,OB=6

∵△OCA∽△OBC
∴OC2=OA•OB=12即OC=2
| 3 |
而
| OB |
| OA |
| OC |
| OA |
2
| ||
| 2 |
| 3 |
| BC |
| AC |
| 3 |
(2)因为C是BP的中点
∴OC=BC从而C点的横坐标为3
又OC=2
| 3 |
| 3 |
设直线BP的解析式为y=kx+b,
因其过点B(6,0),C(3,
| 3 |
则有
|
∴
|
∴y=-
| ||
| 3 |
| 3 |
又点C(3,
| 3 |
∴
| 3 |
∴a=-
| ||
| 3 |
∴抛物线解析式为:y=-
| ||
| 3 |
8
| ||
| 3 |
| 3 |
点评:本题考查了二次函数解析式的确定、函数图象交点、相似三角形的性质等知识点.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
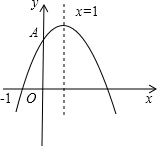 如图,开口向下的抛物线y=ax2+hx+c交y轴的正半轴于点A,对称轴是直线x=1,则下列结论正确的是( )
如图,开口向下的抛物线y=ax2+hx+c交y轴的正半轴于点A,对称轴是直线x=1,则下列结论正确的是( )| A、a+2b+4c<0 | B、c<0 | C、2a+b-c=0 | D、b=-2a |
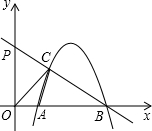 OCA∽△OBC.
OCA∽△OBC.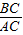 的值;
的值;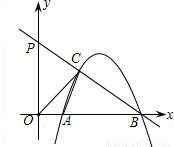
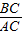 的值;
的值;