Question

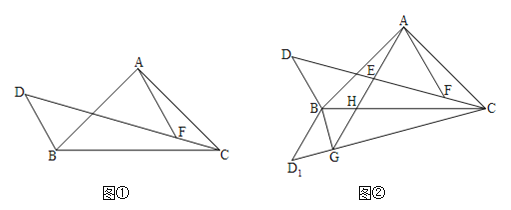
【题目】已知△ABC，AB=AC，∠BAC=90°，D为△ABC外部一点，∠BDC=45°，点F在CD上且AF∥DB．

（1）如图①，求证：；

（2）如图②，将△BCD沿BC翻折得到△BCD1，过点B作BG⊥CD1，垂足为G，连接AG交CD于E，交BC于H．若AF=，∠BCD=15°，求AG的长度．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）过点A作AM⊥AF，交DC于点M，连接BM，利用平行线的性质得到∠AMF=45°，从而得到△AMF是等腰直角三角形，MF=，然后利用AAS定理证得△ABM≌△ACF，然后根据全等三角形的性质得出∠AMB=∠AFC=180°-∠AFM=135°，再结合已知条件求得△BDM是等腰直角三角形，，从而使问题得解；

（2）过点A作AM⊥AF，交DC于点M，连接BM，过点A作AN⊥CD，AK⊥CG，根据（1）中的证明，通过利用等腰直角三角形及折叠的性质得到CD=C D1=，∠D=∠D1=45°，∠DCB=∠D1CB=15°，BC平分∠DCD1，然后利用含30°直角三角形的性质，求得，，最后利用勾股定理求解．

解：（1）如图1，过点A作AM⊥AF，交DC于点M，连接BM

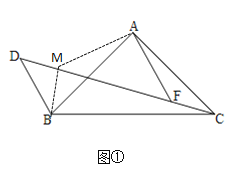
∵∠BDC=45°，且AF∥DB

∴∠AFM=45°

又∵AM⊥AF，∴∠MAF=90°

∴∠AMF=∠AFM=45°

∴AM=AF，即△AMF是等腰直角三角形

∴MF=

又因为∠BAC=90°，∠MAF=90°

∴∠MAB+∠BAF=∠FAC+∠BAF=90°

∴∠MAB =∠FAC

又∵AB=AC

∴△ABM≌△ACF

∴∠AMB=∠AFC=180°-∠AFM=135°

所以∠BMC=90°

又因为∠BDC=45°

∴△BDM是等腰直角三角形

∴

∴DF-MF=DM

即；

（2）如图2，过点A作AM⊥AF，交DC于点M，连接BM，过点A作AN⊥CD，AK⊥CG

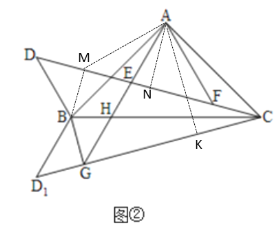
由（1）可知△BDM和△AMF是等腰直角三角形， △ABM≌△ACF

∴AM=AF=，MF=，∠AMF=45°

又∵AN⊥CD

∴

∵∠BCD=15°，∴在Rt△ANC中，∠CAN=30°

∴AC=2AN=2，CN=

又∵等腰直角△AMF中，AN⊥MF，

∴MN=NF

∵△ABM≌△ACF且△BDM是等腰直角三角形

∴BM=DM=CF

∴MN+DM=NF+CF

∴CD=，DM=BM=CF=

又由折叠性质可知，CD=C D1=，∠D=∠D1=45°，∠DCB=∠D1CB=15°，BC平分∠DCD1

∴∠ACK=60°，在Rt△ACK中，∠CAK=30°

∴，

∵BG⊥CD1，BM⊥CD

∴BG=D1G=，CG=

∴GK=CG-CK=

∴在Rt△AGK中，．