题目内容
(本题满分10分)
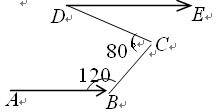
如图,如果AB∥CD,AE平分∠BAC,CE平分∠ACD,你能判定AE与CE垂直吗?为什么?
如图,如果AB∥CD,AE平分∠BAC,CE平分∠ACD,你能判定AE与CE垂直吗?为什么?

(本题满分10分)答案参照教参264页.
考点:
分析:根据两直线平行,同旁内角互补可得∠BAC+∠ACD=180°,再根据角平分线的定义可得∠EAC= ∠BAC,∠ACE=
∠BAC,∠ACE= ∠ACD,然后求出∠EAC+∠ACE=
∠ACD,然后求出∠EAC+∠ACE=
 (∠BAC+∠ACD)=90°,然后求出∠AEC=90°,再根据垂直的定义解答.
(∠BAC+∠ACD)=90°,然后求出∠AEC=90°,再根据垂直的定义解答.
解答:证明:AE⊥CE.理由是:
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠EAC= ∠BAC,∠ACE=
∠BAC,∠ACE= ∠ACD,
∠ACD,
∴∠EAC+∠ACE= (∠BAC+∠ACD)=90°,
(∠BAC+∠ACD)=90°,
∴∠AEC=180°-(∠EAC+∠ACE)=90°,
∴AE⊥CE.
点评:本题考查了两直线平行,同旁内角互补的性质,角平分线的定义,垂直的定义,熟记性质是解题的关键.
分析:根据两直线平行,同旁内角互补可得∠BAC+∠ACD=180°,再根据角平分线的定义可得∠EAC=
 ∠BAC,∠ACE=
∠BAC,∠ACE= ∠ACD,然后求出∠EAC+∠ACE=
∠ACD,然后求出∠EAC+∠ACE= (∠BAC+∠ACD)=90°,然后求出∠AEC=90°,再根据垂直的定义解答.
(∠BAC+∠ACD)=90°,然后求出∠AEC=90°,再根据垂直的定义解答.解答:证明:AE⊥CE.理由是:
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠EAC=
 ∠BAC,∠ACE=
∠BAC,∠ACE= ∠ACD,
∠ACD,∴∠EAC+∠ACE=
 (∠BAC+∠ACD)=90°,
(∠BAC+∠ACD)=90°,∴∠AEC=180°-(∠EAC+∠ACE)=90°,
∴AE⊥CE.
点评:本题考查了两直线平行,同旁内角互补的性质,角平分线的定义,垂直的定义,熟记性质是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

 处,使斜边CD∥AB.则
处,使斜边CD∥AB.则 值为 .
值为 .