题目内容
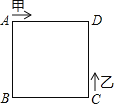
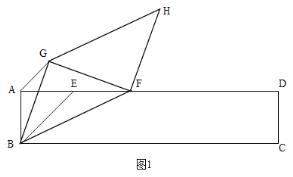
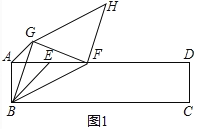
【题目】如图,矩形ABCD,AB=2,BC=10,点E为AD上一点,且AE=AB,点F从点E出发,向终点D运动,速度为1cm/s,以BF为斜边在BF上方作等腰直角△BFG,以BG,BF为邻边作BFHG,连接AG.设点F的运动时间为t秒.
(1)试说明:△ABG∽△EBF;
(2)当点H落在直线CD上时,求t 的值;
(3)点F从E运动到D的过程中,直接写出HC的最小值.

【答案】(1)证明见解析;(2)![]() ;(3)HC最小值是
;(3)HC最小值是![]()
【解析】
(1)根据两边成比例夹角相等即可证明两三角形相似;
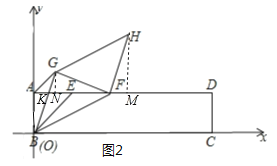
(2)构建如图2平面直角坐标系,作HM⊥AD于M,GN⊥AD于N.设AM交BG于K.首先证明△GFN≌△FHM,想办法求出点H的坐标,构建方程即可解决问题;
(3)由(2)可知H(2![]() t,4
t,4![]() t),令x=2
t),令x=2![]() t,y=4
t,y=4![]() t,消去t得到y
t,消去t得到y![]() .推出点H在直线y
.推出点H在直线y![]() 上运动,根据垂线段最短即可解决问题.
上运动,根据垂线段最短即可解决问题.
(1)如图1.
∵△ABE,△BGF都是等腰直角三角形,∴![]() .
.
∵∠ABE=∠GBF=45°,∴∠ABG=∠EBF,∴△ABG∽△EBF.
(2)如图2构建如图平面直角坐标系,作HM⊥AD于M,GN⊥AD于N.设AM交BG于K.
∵△GFH是等腰直角三角形,∴FG=FH,∠GNF=∠GFH=∠HMF=90°,∴∠GFN+∠HFM=90°,∠HFM+∠FHM=90°,∴∠GFN=∠FHM,∴△GFN≌△FHM,∴GN=FM,FN=HM.
∵△ABG∽△EBF,∴![]() ,∠AGB=∠EFB.
,∠AGB=∠EFB.
∵∠AKG=∠BKF,∴∠GAN=∠KBF=45°.
∵EF=t,∴AG![]() t,∴AN=GN=FM
t,∴AN=GN=FM![]() t,∴AM=2
t,∴AM=2![]() t,HM=FN=2
t,HM=FN=2![]() t,∴H(2
t,∴H(2![]() t,4
t,4![]() t),当点H在直线CD上时,2
t),当点H在直线CD上时,2![]() t=10,解得:t
t=10,解得:t![]() .
.
(3)由(2)可知H(2![]() t,4
t,4![]() t),令x=2
t),令x=2![]() t,y=4
t,y=4![]() t,消去t得到y
t,消去t得到y![]() ,∴点H在直线y
,∴点H在直线y![]() 上运动,如图3,作CH垂直直线y
上运动,如图3,作CH垂直直线y![]() 垂足为H.
垂足为H.
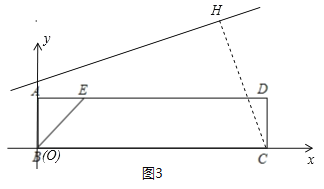
根据垂线段最短可知,此时CH的长最小,易知直线CH的解析式为y=﹣3x+30,由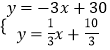 ,解得:
,解得:![]() ,∴H(8,6).
,∴H(8,6).
∵C(10,0),∴CH![]() ,∴HC最小值是2
,∴HC最小值是2![]() .
.