题目内容
已知△ABC中,AB=AC,CD⊥AB于D.
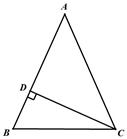
(1)若∠A=40°,求∠DCB的度数;
(2)若AB=10,CD=6,求BD的长.

(1)若∠A=40°,求∠DCB的度数;
(2)若AB=10,CD=6,求BD的长.
(1)20°;(2)2
试题分析:(1)由AB=AC,∠A=40°,可得∠B=70°,再结合CD⊥AB,即可求得结果;
(2)在Rt△ACD中,先根据勾股定理求得AD的长,再结合AB=10,即可求得结果.
(1)∵AB=AC,∠A=40°,
∴∠B=70°
∵CD⊥AB
∴∠CDB=90°
∴∠DCB=20°;
(2)在Rt△ACD中,AC=AB=10,CD=6
∴AD=
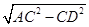 =8
=8∴BD=AB-AD=2.
点评:解答本题的关键是熟练掌握等腰三角形的两个底角相等;三角形的内角和为180°.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

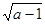 +b
+b -4b+4=0,求c的取值范围。
-4b+4=0,求c的取值范围。 ABC中,
ABC中,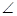 BAC=90
BAC=90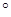 ,
, BC于D,则DC= 。
BC于D,则DC= 。