Question

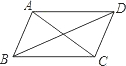
如图：菱形ABCD的对角线AC、BD交于点O，且AC=16，BD=12，求菱形ABCD的高DH的长是（　　）

A．10

B．96

C．9.6

D．以上都不对

Answer 1

∵四边形ABCD是菱形，AC=16，BD=12，
∴AC⊥BD，AO=OC=

1

2

AC=8，BO=BD=

1

2

BD=6，
在Rt△AOB中，由勾股定理得：AB=

AO2+BO2

=10，
∵S_菱形ABCD=

1

2

×AC×BD=AB×DH，
∴

1

2

×16×12=10DH，
∴DH=9.6，
故选C．