题目内容
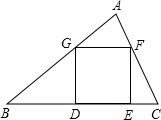 如图,已知正方形内接于△ABC,△AFG的面积为1,△BDG的面积为3,△CEF的面积为1,则正方形DEFG的边长为
如图,已知正方形内接于△ABC,△AFG的面积为1,△BDG的面积为3,△CEF的面积为1,则正方形DEFG的边长为分析:设正方形边长为x,找到△ABC的面积等于△AGF和△BDG和△CEF和正方形DEFG的面积和的等量关系,列出方程求解.
解答: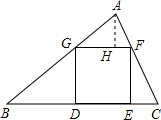 解:作AH⊥FG,
解:作AH⊥FG,
则AH为△AFG中FG边上的高,
设DE=x,AH=y,
∵S△BDG=3,S△AGF=S△FEC=1,即
AH×FG=
CE×EF=1,
∴BD=3y,CE=AH=y,
∵FG∥BC,
∴△AGF∽△ABC,
∴
=
,即
=
,
解得x=2y,
由
CE×EF=1,得
•y•2y=1,
解得y=1,
∴x=2y=2,
故正方形DEFG边长为2.
故答案为:2.
 解:作AH⊥FG,
解:作AH⊥FG,则AH为△AFG中FG边上的高,
设DE=x,AH=y,
∵S△BDG=3,S△AGF=S△FEC=1,即
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=3y,CE=AH=y,
∵FG∥BC,
∴△AGF∽△ABC,
∴
| AH |
| AH+x |
| GF |
| BC |
| y |
| x+y |
| x |
| x+4y |
解得x=2y,
由
| 1 |
| 2 |
| 1 |
| 2 |
解得y=1,
∴x=2y=2,
故正方形DEFG边长为2.
故答案为:2.
点评:本题考查了正方形四边相等,且面积等于边长的平方,本题中找到△ABC的面积等于△AGF和△BDG和△CEF和正方形DEFG的面积和的等量关系是解决本题的关键.

练习册系列答案
相关题目
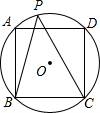 已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP=
已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP= 已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于( )
已知正方形内接于⊙O,P是劣弧AD上任意一点,(如图),则∠ABP+∠DCP等于( )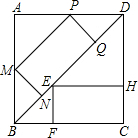 如图,已知正方形ABCD中,点E、N是对角线BD上两动点,过这两个动点作矩形EFCH,MNQP,分别内接于△BCD和△ABD,设矩形EFCH,MNQP的周长分别为m1,m2,则m1,m2的大小关系为( )
如图,已知正方形ABCD中,点E、N是对角线BD上两动点,过这两个动点作矩形EFCH,MNQP,分别内接于△BCD和△ABD,设矩形EFCH,MNQP的周长分别为m1,m2,则m1,m2的大小关系为( ) 如图,已知正方形内接于△ABC,△AFG的面积为1,△BDG的面积为3,△CEF的面积为1,则正方形DEFG的边长为________.
如图,已知正方形内接于△ABC,△AFG的面积为1,△BDG的面积为3,△CEF的面积为1,则正方形DEFG的边长为________.