Question

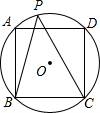已知正方形内接于⊙O，P是劣弧AD上任意一点，（如图），则∠ABP+∠DCP=

45°

．

Answer 1

分析：首先连接OA，OP，OD，由正方形内接于⊙O，即可求得∠AOD的度数，又由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可得∠ABP=

1

2

∠AOP，∠DCP=

1

2

∠DOP，继而求得答案．

解答：解：连接OA，OP，OD，
∵正方形内接于⊙O，
∴∠AOD=90°，
∴∠ABP=

1

2

∠AOP，∠DCP=

1

2

∠DOP，
∴∠ABP+∠DCP=

1

2

∠AOP+

1

2

∠DOP=

1

2

∠AOD=45°．
故答案为：45°．

点评：此题考查了圆周角定理与圆的内接正方形的性质．此题难度不大，注意掌握辅助线的作法，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．