题目内容
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
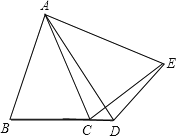
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
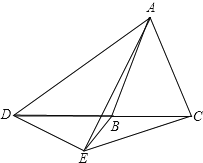
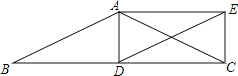
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

【答案】(1)、90°;(2)、①、α+β=180°;理由见解析;②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
【解析】
试题分析:(1)、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出∠BCE=90°;(2)、①、、根据∠BAC=∠DAE得出∠BAD=∠CAE,然后利用SAS判定△ABD和△ACE全等,从而得出∠B=∠ACE,则∠B+∠ACB=∠ACE+∠ACB,从而得出α+β=180°;②、根据题意分别画出两个图形,然后分别进行计算得出答案,当点D在射线BC上时,α+β=180°;当点D在射线BC的反向延长线上时,α=β.
试题解析:(1)、90°.
∵∠BAC=∠DAE, ∴∠BAC-∠DAC=∠DAE-∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS),
∴∠B=∠ACE. ∴∠B+∠ACB=∠ACE+∠ACB, ∴∠BCE=∠B+∠ACB, 又∵∠BAC=90° ∴∠BCE=90°
(2)、①α+β=180°,
∵∠BAC=∠DAE, ∴∠BAD+∠DAC=∠EAC+∠DAC. 即∠BAD=∠CAE.
在△ABD与△ACE中,AB=AC,∠BAD=∠CAE,AD=AE ∴△ABD≌△ACE(SAS), ∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB. ∴∠B+∠ACB=β, ∵α+∠B+∠ACB=180°, ∴α+β=180°;
②、当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.