题目内容
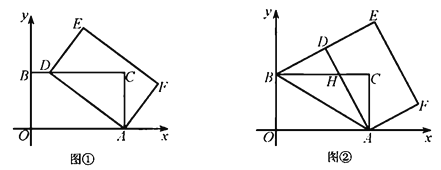
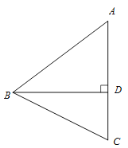
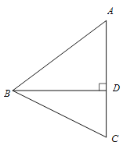
【题目】如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE.
(1)①依题意补全图形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.
【答案】(1) ①见解析;②![]() ;(2)2
;(2)2![]() .
.
【解析】(1) ①以点D为圆心,CD为半径作弧,与AD的交点为E,连接BE;②由等腰三角形性质求得∠ABC=∠ACB=90°-![]() .再由轴对称性质得BE=BC,可证∠BEC=∠ACB=90°-
.再由轴对称性质得BE=BC,可证∠BEC=∠ACB=90°-![]() ,进一步得∠DBE=90°-∠BEC=
,进一步得∠DBE=90°-∠BEC=![]() .(2)作FG⊥AC于G,证FG∥BD,再证FG是三角形BED的中位线,得
.(2)作FG⊥AC于G,证FG∥BD,再证FG是三角形BED的中位线,得![]() ,由DE=2AE,得AE=EG=DG.设AE=EG=DG=x,则AB=AC=5x.由勾股定理得BD=4x;再由BD=4,求得x =1,在直角三角形AFG中,利用勾股定理可求得AF=
,由DE=2AE,得AE=EG=DG.设AE=EG=DG=x,则AB=AC=5x.由勾股定理得BD=4x;再由BD=4,求得x =1,在直角三角形AFG中,利用勾股定理可求得AF=![]() .
.

练习册系列答案
相关题目