题目内容
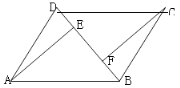
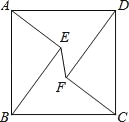
【题目】如图,在正方形ABCD中,AD=5,点E,F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为_____.
【答案】![]()
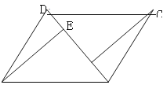
【解析】分析:延长AE交DF于G,再根据全等三角形的判定得出△AGD与△ABE全等,得出AG=BE=4,由AE=3,得出EG=1,同理得出GF=1,再根据勾股定理得出EF的长.
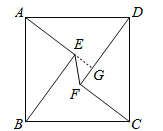
详解:延长AE交DF于G,如图, ∵AB=5,AE=3,BE=4,
∴△ABE是直角三角形,
同理可得△DFC是直角三角形,可得△AGD是直角三角形,
∴∠ABE+∠BAE=∠DAE+∠BAE,∴∠GAD=∠EBA,
同理可得:∠ADG=∠BAE.
在△AGD和△BAE中,∵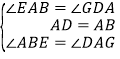 ,
,
∴△AGD≌△BAE(ASA),
∴AG=BE=4,DG=AE=3,∴EG=4﹣3=1,
同理可得:GF=1,∴EF=![]() .
.
故答案为:![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目