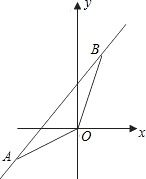
题目内容
如图,已知一次函数 的图象经过
的图象经过 ,
, 两点,并且交x轴于点C,交y轴于点D.
两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求 的值;
的值;
(3)求证: .
.
【答案】
(1) ;(2)
;(2) ;(3)取点A关于原点的对称点
;(3)取点A关于原点的对称点 ,则问题转化为求证
,则问题转化为求证 .由勾股定理可得,
.由勾股定理可得, ,
, ,
,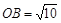 ,即可得到
,即可得到 ,则△EOB是等腰直角三角形,问题得证.
,则△EOB是等腰直角三角形,问题得证.
【解析】
试题分析:(1)由一次函数的图象经过 ,
, 两点根据待定系数法求解即可;
两点根据待定系数法求解即可;
(2)先求得一次函数的图象与坐标轴的交点坐标,即可得到OD、OC的长,再根据正切函数的定义求解即可;
(3)取点A关于原点的对称点 ,则问题转化为求证
,则问题转化为求证 .由勾股定理可得,
.由勾股定理可得, ,
, ,
,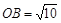 ,即可得到
,即可得到 ,则△EOB是等腰直角三角形,问题得证.
,则△EOB是等腰直角三角形,问题得证.
(1)由已知可得 ,解得
,解得 ,
,
所以一次函数的解析式为
(2)先求出一次函数 与坐标轴的交点
与坐标轴的交点 ,
, .
.
∴在 △OCD中,
△OCD中, ,
, ,
,
∴
 .
.
(3)取点A关于原点的对称点 ,则问题转化为求证
,则问题转化为求证 .由勾股定理可得,
.由勾股定理可得,

 ,
, ,
,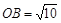 ,
,
∵ ,
,
∴△EOB是等腰直角三角形.
∴ .
.
∴ .
.
考点:一次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点.
如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点. 如图,已知一次函数的图象经过点A(-1,0)、B(0,2).
如图,已知一次函数的图象经过点A(-1,0)、B(0,2). 在第一象限,CD⊥x轴于D,若OA=OB=OD=1.
在第一象限,CD⊥x轴于D,若OA=OB=OD=1. 的图象经过
的图象经过 ,
, 两点,并且交x轴于点C,交y轴于点D.
两点,并且交x轴于点C,交y轴于点D.
 的值;
的值; .
. 的图象与
的图象与 轴、
轴、 轴分别交于A、B两点且与反比例函数
轴分别交于A、B两点且与反比例函数 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥ ,A B =
,A B =  ,C D =
,C D = 

