题目内容
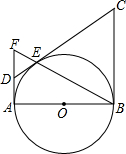 (1998•海淀区)已知:如图,AB是⊙O的直径,线段AF和⊙O切于点A,D是AF的中点,BF交⊙O于点E,过B点的切线与DE的延长线交于点C.
(1998•海淀区)已知:如图,AB是⊙O的直径,线段AF和⊙O切于点A,D是AF的中点,BF交⊙O于点E,过B点的切线与DE的延长线交于点C.(1)求证:CD与⊙O相切.
(2)若tan∠BEC=2,BE+CD=8+5
| 5 |
分析:(1)连接AE、OE、OD,可证△ADO≌△EDO,继而可得∠DEO=90°,这样可证得CD与⊙O相切.
(2)设AE=x,则BE=2x,根据切线的性质,勾股定理和三角形的相似,表示出有关线段的长度,然后利用BE+CD=8+5
解出x,继而求四边形ABCD的周长.
(2)设AE=x,则BE=2x,根据切线的性质,勾股定理和三角形的相似,表示出有关线段的长度,然后利用BE+CD=8+5
| 5 |
解答:解:
连接AE、OE、OD,
∵AB是⊙O的直径,
∴∠AEB=90°,则∠AEF=90°,
在Rt△AEF中,
∵D是AF的中点,
∴DE=FD=AD,
在△ADO与△EDO中,
,
∴△ADO≌△EDO,
∵线段AF和⊙O切于点A,
∴∠DAO=∠DEO=90°,
∴CD与⊙O相切.
(2)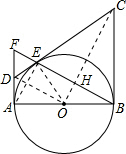
连接OC交EB于点H,
∵CE、CB为⊙O的切线,
∴OC⊥EB,
易得△BOC∽△HBC,
∴∠COB=∠CBE,
∵CE、CB是⊙O的切线,
∴∠CEB=∠EAB=∠CBE,
∵tan∠BEC=2,设AE=x,则BE=2x,
∴AB=
=
x,OB=
x,
∵∠COB=∠CBE=∠CEB,
∴CB=
x=CE,
在Rt△FAB中,AB=
x,AF=
x,
则AD=
x=DE,
∴CD=CE+ED=
x,
∵BE+CD=8+5
,
代入可得2x+
x=8+5
,
解得x=4,
∴四边形ABCD的周长=AD+DC+BC+AB=2DC+AB=2×4×
+
×4=14
.

连接AE、OE、OD,
∵AB是⊙O的直径,
∴∠AEB=90°,则∠AEF=90°,
在Rt△AEF中,
∵D是AF的中点,
∴DE=FD=AD,
在△ADO与△EDO中,
|
∴△ADO≌△EDO,
∵线段AF和⊙O切于点A,
∴∠DAO=∠DEO=90°,
∴CD与⊙O相切.
(2)

连接OC交EB于点H,
∵CE、CB为⊙O的切线,
∴OC⊥EB,
易得△BOC∽△HBC,
∴∠COB=∠CBE,
∵CE、CB是⊙O的切线,
∴∠CEB=∠EAB=∠CBE,
∵tan∠BEC=2,设AE=x,则BE=2x,
∴AB=
| AE2+BE2 |
| 5 |
| ||
| 2 |
∵∠COB=∠CBE=∠CEB,
∴CB=
| 5 |
在Rt△FAB中,AB=
| 5 |
| ||
| 2 |
则AD=
| ||
| 4 |
∴CD=CE+ED=
5
| ||
| 4 |
∵BE+CD=8+5
| 5 |
代入可得2x+
5
| ||
| 4 |
| 5 |
解得x=4,
∴四边形ABCD的周长=AD+DC+BC+AB=2DC+AB=2×4×
5
| ||
| 4 |
| 5 |
| 5 |
点评:本题属于圆的综合题,涉及了切线的判定与性质,相似三角形的判定与性质及勾股定理的应用,解答本题的关键是熟练掌握各知识点,要求同学们仔细思考,将所学知识融会贯通.

练习册系列答案
相关题目