题目内容
正三角形的内切圆的面积与外接圆的面积之比是（ ）A．1：5
B．1：4
C．1：3
D．1：2
【答案】分析：首先根据题意作图，易得点O即是△ABC的外心，又是⊙O的内心，且外接圆的半径为OB，内接圆的半径为OD，AD⊥BC，然后由直角三角形的性质，得到OD=
OB，继而求得答案．
解答：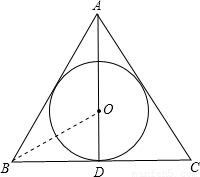
解：如图，△ABC为等边三角形，AD为角平分线，⊙O为△ABC的内切圆，连OB，如图，
∵△ABC为等边三角形，⊙O为△ABC的内切圆，
∴点O即是△ABC的外心，又是⊙O的内心，且外接圆的半径为OB，内接圆的半径为OD，AD⊥BC，
∴∠OBC=30°，
在Rt△OBD中，OD=
OB，
∴正三角形的内切圆的面积与外接圆的面积之比是：πOD2：πOB2=1：4．
故选B．
点评：此题考查了三角形的内切圆与外接圆的性质以及等边三角形的性质．此题难度适中，注意掌握数形结合思想的应用．
OB，继而求得答案．解答：
解：如图，△ABC为等边三角形，AD为角平分线，⊙O为△ABC的内切圆，连OB，如图，∵△ABC为等边三角形，⊙O为△ABC的内切圆，
∴点O即是△ABC的外心，又是⊙O的内心，且外接圆的半径为OB，内接圆的半径为OD，AD⊥BC，
∴∠OBC=30°，
在Rt△OBD中，OD=
OB，∴正三角形的内切圆的面积与外接圆的面积之比是：πOD2：πOB2=1：4．
故选B．
点评：此题考查了三角形的内切圆与外接圆的性质以及等边三角形的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
，AB=2BC．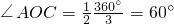
，OC=r，∴AC=r•tan60°，AB=2r•tan60°，∴
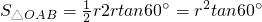，∴S正三角形=3S△OAB=3r2•tan60°．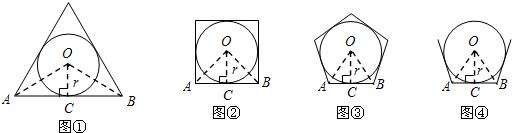
，AB=2BC．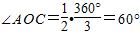
，OC=r，∴AC=r•tan60°，AB=2r•tan60°，∴
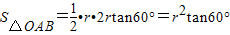，∴S正三角形=3S△OAB=3r2•tan60°．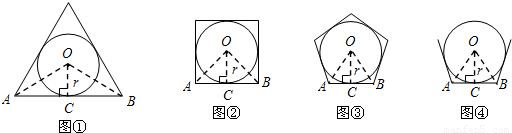
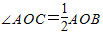，AB=2BC．
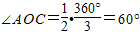，OC=r，∴AC=r•tan60°，AB=2r•tan60°，∴
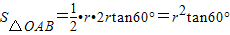，∴S正三角形=3S△OAB=3r2•tan60°．