题目内容
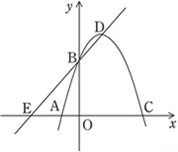
【题目】如图(1),在平面直角坐标系中,抛物线![]() 经过
经过
A(-1,0)、B(0,3)两点,与![]() 轴交于另一点C,顶点为D.
轴交于另一点C,顶点为D.
(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与![]() 轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
(3)如图(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.
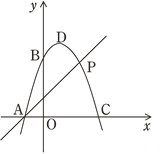
图(1) 图(2)
【答案】(1)抛物线的解析式为: ![]() ,
, ![]() ,D(1,4) ;
,D(1,4) ;
(2)点F的坐标为(2,3);
(3)S△PQA的最大面积为![]() ,此时Q
,此时Q![]() .
.
【解析】试题分析:(1)、将A、B两点的坐标代入,利用待定系数法求出函数解析式,根据方程的思想求出点C的坐标,将二次函数进行配方,从而得出点D的坐标;(2)、设直线BD的解析式为y=kx+b,将B、D两点坐标代入求出函数解析式,从而得出点E的坐标,根据平行四边形的性质得出BF=AE=2,根据点F的横坐标以及函数解析式得出点F的坐标;(3)、设Q![]() , 作PS⊥x轴,QR⊥x轴于点S、R,根据题意将AR、QR、PS、RS和AS用含m的代数式表示出来,根据S△PQA=S四边形PSRQ+S△QRA-S△PSA得出关于m的函数解析式,将函数解析式进行配方,从而得出最大值和点Q的坐标.
, 作PS⊥x轴,QR⊥x轴于点S、R,根据题意将AR、QR、PS、RS和AS用含m的代数式表示出来,根据S△PQA=S四边形PSRQ+S△QRA-S△PSA得出关于m的函数解析式,将函数解析式进行配方,从而得出最大值和点Q的坐标.
试题解析:(1)∵抛物线![]() 经过A(-1,0)、B(0,3)两点,
经过A(-1,0)、B(0,3)两点,
∴ ![]()
![]() 解得:
解得: ![]()
抛物线的解析式为: ![]()
∵由![]() ,解得:
,解得: ![]() ∴
∴![]()
∵由![]()
![]() ∴D(1,4)
∴D(1,4)
(2)∵四边形AEBF是平行四边形, ∴BF=AE. 设直线BD的解析式为y=kx+b,则
∵B(0,3),D(1,4) ∴n=3 k+n=4 解得:k=1,n=3
∴直线BD的解析式为y=x+3 当y=0时,x=-3 ∴E(-3,0), ∴OE=3,
∵A(-1,0) ∴OA=1, ∴AE=2 ∴BF=2,
∴F的横坐标为2, ∴y=3, ∴F(2,3);
(3)如图,设Q![]() , 作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
, 作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
∴AR= ![]() ,QR=
,QR=![]() , PS=3,RS=2-m,AS=3
, PS=3,RS=2-m,AS=3
∴S△PQA=S四边形PSRQ+S△QRA-S△PSA=![]()
=![]()
∴S△PQA=![]()
∴当![]() 时,S△PQA的最大面积为
时,S△PQA的最大面积为![]() , 此时Q
, 此时Q![]()


【题目】滨州苏宁电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1720元 |
第二周 | 4台 | 10台 | 2960 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t , 估计当x=3.2千克时,t的值为( )
A.140
B.138
C.148
D.160