Question

【题目】已知：如图，在四边形ABCD中，AB⊥BD，AD∥BC，∠ADB=45°，∠C=60°，AB=.

求四边形ABCD的周长.

Answer 1

【答案】

【解析】解： ∵ AB⊥BD ，∴∠ABD=90°.

在Rt△ABD中，∠ABD=90°，∠ADB=45°，AB=.∴∠DAB=45°.

∴∠DAB=∠ADB.∴ AB=BD=

∴由勾股定理解得：AD=.

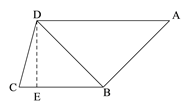
∵ AD∥BC , ∴∠ADB=∠DBC=45°.

过点D作DE⊥BC交BC于点E.

∴ ∠DEB=∠DEC=90°.

在Rt△DEB中，∠DEB=90°，∠DBC =45°，AC=2.

∴∠BDE=45°, sin∠DBC =.

∴∠DBC=∠BDE，DE= .∴ BE=DE=.

在Rt△DEC中，∠DEC=90°，∠C=60°.

∵ .

∴CD=2,CE=1.

∴BC=BE+CE= +1 .

∴四边形ABCD的周长=AB+BC+CD+AD=++