题目内容
如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AB于E.

(1)证明△PAE∽△CDP;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设AP=x,BE=y,求y与x的函数关系式及y的取值范围;
(3)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由.

(1)证明△PAE∽△CDP;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,设AP=x,BE=y,求y与x的函数关系式及y的取值范围;
(3)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由.
(1)证明见解析;(2)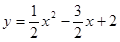 ,y<2;(3)存在,AP+AQ=3,理由见解析.
,y<2;(3)存在,AP+AQ=3,理由见解析.
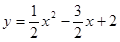 ,y<2;(3)存在,AP+AQ=3,理由见解析.
,y<2;(3)存在,AP+AQ=3,理由见解析.试题分析:(1)利用矩形的性质可以得到∠A=∠D,利用PE⊥PC可以得到∠APE=∠DCP,从而证明两三角形相似;
(2)利用上题证得的三角形相似,列出比例式,进而得到两个变量之间的函数关系;
(3)假设存在符合条件的Q点,由于PE⊥PC,且四边形ABCD是矩形,易证得△APE∽△DCP,可得AP•PD=AE•CD,同理可通过△AQE∽△DCQ得到AQ•QD=AE•DC,则AP•PD=AQ•QD,分别用PD、QD表示出AP、AQ,将所得等式进行适当变形即可求得AP、AQ的数量关系.
试题解析:(1)∵四边形ABCD为矩形,∴∠A=∠D=90°,∴∠AEP+∠APE=90°,
∵PE⊥PC,∴∠APE+∠CPD=90°,
∴∠AEP=∠DPC,
∴△PAE∽△CDP;
(2)(解法一)∵AP=x,BE=y,∴DP=3-x,AE=2-y. 4分
∵△PAE∽△CDP,∴
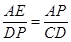 , 5分
, 5分即
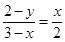 ,∴
,∴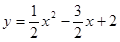 . 6分
. 6分(解法二)∵AP=x,BE=y,∴DP=3-x,AE=2-y. 4分
∵∠A=∠D=90°,∴tan∠AEP=
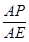 , tan∠DPC=
, tan∠DPC=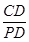 ,
, ∵∠AEP=∠DPC,∴tan∠AEP= tan∠DPC. ∴
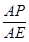 =
=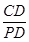 ,
,即
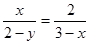 ,∴
,∴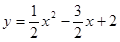 .
.(解法三)∵AP=x,BE=y,∴DP=3-x,AE=2-y.
如图1,连结CE, ∵∠A=∠B=∠D="90°,"

∴AE2+AP2=PE2,PD2+CD2=CP2,BE2+BC2=CE2,
又∵∠CPE=90°,∴PE2+CP2=CE2,
∴AE2+AP2+PD2+CD2=BE2+BC2,
即(2-y)2+x2+(3-x)2+22=y2+32,整理得:
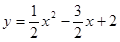 .
.∵
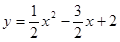 =
=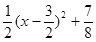 ,
,∴当
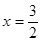 时,y有最小值,y的最小值为
时,y有最小值,y的最小值为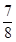 ,
,又∵点E在AB上运动(显然点E与点A不重合),且AB=2,
∴
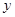 <2
<2综上所述,
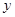 的取值范围是
的取值范围是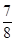 ≤
≤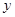 <2;
<2;(3)存在,理由如下:
如图2,假设存在这样的点Q,使得QC⊥QE.
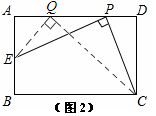
由(1)得:△PAE∽△CDP,
∴
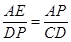 ,
,∴
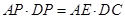 ,
,∵QC⊥QE,∠D=90°,
∴∠AQE+∠DQC=90°,∠DQC+∠DCQ=90°,
∴∠AQE=∠DCQ.
又∵∠A=∠D=90°,
∴△QAE∽△CDQ,
∴
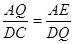 ,
,∴
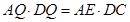
∴
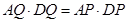 ,
,即
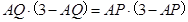 ,
,∴
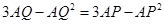 ,
,∴
 ,
,∴
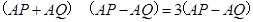 .
.∵AP≠AQ,∴AP+AQ=3.又∵AP≠AQ,∴AP≠
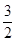 ,即P不能是AD的中点,
,即P不能是AD的中点,∴当P是AD的中点时,满足条件的Q点不存在,
故当P不是AD的中点时,总存在这样的点Q满足条件,此时AP+AQ=3.
考点: 相似三与性质角形的判定;矩形的性质.

练习册系列答案
相关题目
 ,则
,则 ____________.
____________.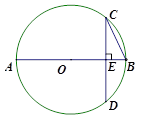
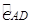 上一点(不与点C、A、D重合),连接BP与CD交于点G.
上一点(不与点C、A、D重合),连接BP与CD交于点G. 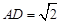 ,
,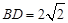 ,求AB的值.
,求AB的值.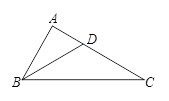

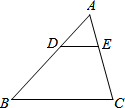
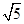
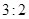 B.
B.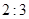 C.
C.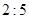 D.
D.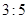
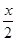 =
=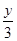 ,那么
,那么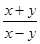 的值是( )
的值是( )