题目内容
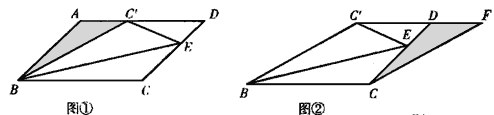
【题目】如图①,四边形ABCD为平行四边形,E在CD边上,将△BCE沿BE翻折,点C刚好落在AB边上的点C′处
(1)在图①中,请直接写出四对相等的线段;
(2)将图①中的△ABC′剪下并拼接在图②中△DCF的位置上(其中△ABC′的三个顶点A、B、C′分别与△DCF的三个顶点D、C、F重合,并且图②的点C′、D、F在同一直线上)试证明图②中的四边形BCFC′是菱形.
【答案】(1)、AB=CD,AD=BC,BC=BC′,EC=EC′;(2)、证明过程见解析
【解析】
试题分析:(1)、根据平行四边形的性质以及折叠图形的性质得出答案;(2)、根据平行四边形的性质得出BC=AD,BC∥C′D,根据图形得出△ABC′≌△DCF,然后根据线段之间的关系得出BC= C′F,从而得出四边形BCFC′为平行四边形,根据折叠图形的性质得出BC=BC′,从而得出菱形.
试题解析:(1)AB=CD,AD=BC,BC=BC′,EC=EC′
(2)、在图①中, ∵四边形ABCD为平行四边形,∴BC=AD,BC∥C′D
在图①与图②中,由题意知:△ABC′≌△DCF,
∴AC′=DF
∴AC′+C′D= C′D +DF
∴AD= C′F,即得BC= C′F
∵BC∥C′F,∴四边形BCFC′为平行四边形
又由折叠的性质得:BC=BC′,
∴四边形BCFC′为菱形。

练习册系列答案
相关题目