题目内容
【题目】
问题探究:(1)已知:如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE丄DH于点O,求证:AE=DH
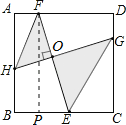
类比探究:(2)已知:如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,则线段EF与HG有什么数量关系,并说明理由;
拓展应用:(3)已知:如图3,在(2)问条件下,若HF∥GE,BE=EC=2,EO=2FO,求HG的长.
【答案】(1)见解析;(2)EF=GH,理由见解析;(3)GH=![]() .
.
【解析】
试题分析:(1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;
(2)EF=GH.将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;
(3)易得△AHF∽△CGE,所以![]() ,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=
,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=![]() ,根据(2)①知EF=GH,即可得到结论.
,根据(2)①知EF=GH,即可得到结论.
解:(1)∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO.
∴△ABE≌△DAH(ASA),
∴AE=DH.
(2)EF=GH.
将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.

∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,所以EF=GH;
(3)∵四边形ABCD是正方形,
∴AB∥CD
∴∠AHO=∠CGO
∵FH∥EG
∴∠FHO=∠EGO
∴∠AHF=∠CGE
∴△AHF∽△CGE
∴![]() ,
,
∵EC=2,
∴AF=1,
过F作FP⊥BC于P,
根据勾股定理得EF=![]() =
=![]()
根据(2)知EF=GH,
∴GH=![]() .
.