题目内容
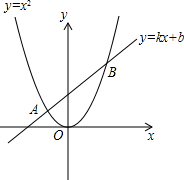 如图,已知直线y=kx+b(k>0)与抛物线y=x2交于A、B两点(A、B两点分别位于第二和第一象限),且A、B两点的纵坐标分别是1和9,则不等式x2-kx-b>0的解集为
如图,已知直线y=kx+b(k>0)与抛物线y=x2交于A、B两点(A、B两点分别位于第二和第一象限),且A、B两点的纵坐标分别是1和9,则不等式x2-kx-b>0的解集为
- A.-1<x<3
- B.x<-1或x>3
- C.1<x<9
- D.x<1或x>9
B
分析:先把不等式整理成x2>kx+b,然后根据抛物线解析式求出点A、B的纵坐标求出横坐标,再找出抛物线图象在直线图象上方的部分的x的取值范围即可得解.
解答:由x2-kx-b>0得x2>kx+b,
∵A、B两点的纵坐标分别是1和9,
∴点A的横坐标为-1,点B的横坐标为3,
当x<-1或x>3时,抛物线图象在直线图象上方,
故不等式x2-kx-b>0的解集为x<-1或x>3.
故选B.
点评:本题考查了二次函数与不等式组,根据图象的上下方关系确定不等式的解集与x的取值范围是解题的关键,数形结合是数学中的重要思想之一.
分析:先把不等式整理成x2>kx+b,然后根据抛物线解析式求出点A、B的纵坐标求出横坐标,再找出抛物线图象在直线图象上方的部分的x的取值范围即可得解.
解答:由x2-kx-b>0得x2>kx+b,
∵A、B两点的纵坐标分别是1和9,
∴点A的横坐标为-1,点B的横坐标为3,
当x<-1或x>3时,抛物线图象在直线图象上方,
故不等式x2-kx-b>0的解集为x<-1或x>3.
故选B.
点评:本题考查了二次函数与不等式组,根据图象的上下方关系确定不等式的解集与x的取值范围是解题的关键,数形结合是数学中的重要思想之一.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
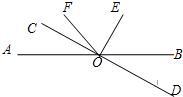 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.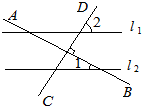 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=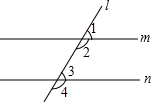 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )