题目内容
【题目】如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
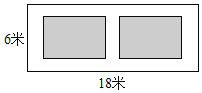
A. 2B. 1C. 8或1D. 8
【答案】B
【解析】
设人行道的宽度为x米,则两块矩形绿地可合成长为(18-3x)米、宽为(6-2x)米的矩形,根据矩形的面积公式结合两块绿地的面积之和为60平方米,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
解:设人行道的宽度为x米,则两块矩形绿地可合成长为(18-3x)米、宽为(6-2x)米的矩形,
根据题意得:(18-3x)(6-2x)=60,
整理得:x2-9x+8=0,
解得:x1=1,x2=8.
∵8>6,
∴x2=8舍去.
故选:B.

练习册系列答案
相关题目
【题目】下列表格是某学校女子排球队队员年龄统计表:
年龄(岁) | 13 | 14 | 15 | 16 |
人数(人) | 1 | 2 | 4 | 5 |
(1)该排球队队员年龄的众数是 岁;
(2)事件“从该排球队随机选择一名队员,其年龄为13岁”发生的概率为 ;
(3)教练決定从年龄为13岁和14岁的A、B、C三名队员中,随机选取两名队员进行“接发球”训练,求队员A、B同时被选中的概率.(树状图或列表法)