题目内容

（1）在实数范围内分解因式：
①9a⁴-4b⁴；
②x²-2

x+3．
（2）比较

与

的大小．

分析：（1）①两次运用平方差公式来因式分解，要分解到无理数范围；
②运用完全平方公式来因式分解，要分解到无理数范围；
（2）先分母有理化再比较大小．

解答：解：（1）①9a⁴-4b⁴=（3a²-2b²）（3a²+2b²）
=（

b）（

b）（3a²+2b²）；
②x²-2

x+3=（x-

）²；
（2）

，

则

＜0
∴

＜

．

点评：一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能再分解为止；比较两个分式，一般采用作差法．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

．
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|x-4|的零点值；
（2）化简代数式|x+2|+|x-4|．

（1）分类讨论是一种重要的数学思想，比如要在实数范围内化简|x-1|可以按x与1的大小关系分三种情况讨论：
①当x＞1时，x-1＞0，则|x-1|=x-1．
②当x=1时，x-1=0，则|x-1|=0．
③当x＜1时，x-1＜0，则|x-1|=

1-x

．
（2）请根据以上思想，在实数范围内比较代数式a与

的大小关系．

阅读下列材料并解决有关问题：我们知道：|x|=

-x(当x＜0时)

0(当x=0时)

x(当x＞0时)

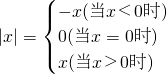，现在我们可以用这一结论来解含有绝对值的方程．例如，解方程|x+1|+|2x-3|=8时，可令x+1=0和2x-3=0，分别求得x=-1和

，（称-1和

分别为|x+1|和|2x-3|的零点值），在实数范围内，零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况：①x＜-1②-1≤x＜

③x≥

，从而解方程|x+1|+|2x-3|=8可分以下三种情况：
①当x＜-1时，原方程可化为-（x+1）-（2x-3）=8，解得x=-2．
②当-1≤x＜

时，原方程可化为（x+1）-（2x-3）=8，解得x=-4，但不符合-1≤x＜

，故舍去．
③当x≥

时，原方程可化为（x+1）+（2x-3）=8，解得x=

．
综上所述，方程|x+1|+|2x-3|=8的解为，x=-2和x=

．
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|3x-1|的零点值．
（2）解方程|x+2|+|3x-1|=9．

阅读下列材料并解决有关问题：
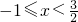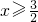我们知道： $数学公式$ ，现在我们可以用这一结论来解含有绝对值的方程．例如，解方程|x+1|+|2x-3|=8时，可令x+1=0和2x-3=0，分别求得x=-1和，（称-1和 $数学公式$ 分别为|x+1|和|2x-3|的零点值），在实数范围内，零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况：①x＜-1② $数学公式$ ③ $数学公式$ ，从而解方程|x+1|+|2x-3|=5可分以下三种情况：
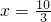①当x＜-1时，原方程可化为-（x+1）-（2x-3）=8，解得x=-2．
②当 $数学公式$ 时，原方程可化为（x+1）-（2x-3）=8，解得x=-4，但不符合 $数学公式$ ，故舍去．
③当 $数学公式$ 时，原方程可化为（x+1）+（2x-3）=8，解得 $数学公式$ ．
综上所述，方程|x+1|+|2x-3|=8的解为，x=-2和 $数学公式$ ．
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|3x-1|的零点值．
（2）解方程|x+2|+|3x-1|=9．

在实数范围内因式分x²-3x+1=______．

试题分类