题目内容
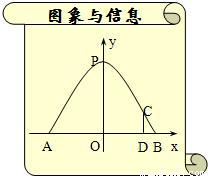
如图所示,已知某一水库大坝的横断面是梯形ABCD,坝顶宽CD=3米,坝高8米,斜边BC的坡度i=1∶3(竖直高度比水平距离),∠A=45°,求坝底AB的宽.

答案:35m#35米
解析:
提示:
解析:
|
解:作 DE⊥AB,CF⊥AB,垂足分别为点E、F,易得四边形DCFE是矩形,所以EF=DC=3米,DE=CF=8米,因为∠A=45°,所以AE=DE=8米.又因为i=1∶3,所以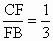 ,FB=3CF=3×8=24(米), ,FB=3CF=3×8=24(米),
所以 AB=AE+EF+FB=8+3+24=35(米). |
提示:
|
进行梯形的上、下底的计算或求梯形的面积时,通常作梯形的两条高,将梯形分成两个直角三角形和一个矩形. |

练习册系列答案
相关题目
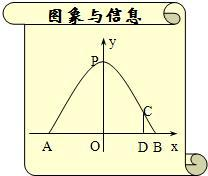 ,垂直地面立起一根1.7m长的木杆,其顶端恰好顶在抛物线形门上C处,建立如图所示的坐标系.
,垂直地面立起一根1.7m长的木杆,其顶端恰好顶在抛物线形门上C处,建立如图所示的坐标系.