Question

如图所示，已知：一抛物线形拱门，其地面宽度AB=18m，小明站在门内，在离门脚B点1m远的点D处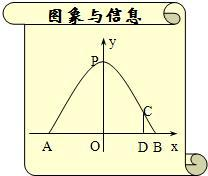，垂直地面立起一根1.7m长的木杆，其顶端恰好顶在抛物线形门上C处，建立如图所示的坐标系．
（1）求出拱门所在抛物线的解析式；
（2）求出该大门的高度OP．

Answer 1

分析：根据抛物线在坐标系的特殊位置，对称轴是y轴，可设拱门所在抛物线的解析式为y=ax²+c，依题意找出B、C两点的坐标，就可以确定抛物线解析式了．对称轴是y轴，最大值就是常数c的值．

解答：解：（1）设拱门所在抛物线的解析式为y=ax²+c，
将C（8，1.7）、B（9，0）两点的坐标代入y=ax²+c中，
得

1.7=64a+c 0=81a+c

，
解得a=-

1

10

，c=8.1，
∴y=-

1

10

x²+8.1；

（2）当x=0时，y=8.1（m）．所以，该大门的高度OP为8.1m．

点评：本题经历选取抛物线解析式的形式，求抛物线解析式，运用解析式解答题目问题，充分体现由实际问题--抛物线--实际问题，体现数学知识的运用价值．