题目内容
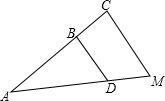
如图,在△ABC中,点D、E分别在边AB、BC上,CD与AE相交于点F,点G在边BC上,DG∥AE, CE=1,BE=3,BD=2,AD=4.
CE=1,BE=3,BD=2,AD=4.
(1)求GE的长;
(2)求
的值;
(3)设DG=x,CF=y,求y关于x的函数解析式,并写出定义域.
 CE=1,BE=3,BD=2,AD=4.
CE=1,BE=3,BD=2,AD=4.(1)求GE的长;
(2)求
| EF |
| FA |
(3)设DG=x,CF=y,求y关于x的函数解析式,并写出定义域.
(1)∵DG∥AE,
∴
=
.(2分)
去分母得:GE•BA=AD•BE,
两边都除以AB得:GE=
,
∵BE=3,BD=2,AD=4,
∴BA=6,
∴GE=
=
=2.(2分)
(2)∵DG∥AE,CE=1,CG=CE+GE=3,
∴
=
=
,(2分)
∵
=
=
=
.(1分)
∴
=
,(1分)
∴
=
.(1分)
(3)∵BG=BE-GE=3-2=1,BC=BE+CE=4,
∴
=
,
=
=
.
∴
=
,(1分)
∵∠B=∠B,
∴△BGD∽△BDC.(1分)
∴
=
=
,
∵DG=x,
∴DC=2x.(1分)
∵EF∥DG,
∴
=
=
,
∴
=
,
∴y=
x.(1分)
∴定义域为1<x<3.(1分)
∴
| GE |
| BE |
| AD |
| BA |
去分母得:GE•BA=AD•BE,
两边都除以AB得:GE=
| BE•AD |
| BA |
∵BE=3,BD=2,AD=4,
∴BA=6,
∴GE=
| BE•AD |
| BA |
| 3×4 |
| 6 |
(2)∵DG∥AE,CE=1,CG=CE+GE=3,
∴
| EF |
| DG |
| CE |
| CG |
| 1 |
| 3 |
∵
| DG |
| AE |
| BD |
| BA |
| 2 |
| 6 |
| 1 |
| 3 |
∴
| EF |
| AE |
| 1 |
| 9 |
∴
| EF |
| FA |
| 1 |
| 8 |
(3)∵BG=BE-GE=3-2=1,BC=BE+CE=4,
∴
| BG |
| BD |
| 1 |
| 2 |
| BD |
| BC |
| 2 |
| 4 |
| 1 |
| 2 |
∴
| BG |
| BD |
| BD |
| BC |
∵∠B=∠B,
∴△BGD∽△BDC.(1分)
∴
| DG |
| DC |
| BG |
| BD |
| 1 |
| 2 |
∵DG=x,
∴DC=2x.(1分)
∵EF∥DG,
∴
| CF |
| CD |
| CE |
| CG |
| 1 |
| 3 |
∴
| y |
| 2x |
| 1 |
| 3 |
∴y=
| 2 |
| 3 |
∴定义域为1<x<3.(1分)

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 ,则OD∶
,则OD∶ =
= 
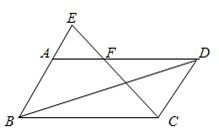
 与正方形
与正方形 的位置如图所示.
的位置如图所示.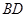 交
交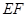 于点
于点 ;
;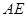 上取一点
上取一点 ,联结
,联结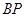 ,
,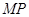 ,使△
,使△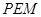 与△
与△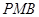 相似;
相似;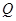 是线段
是线段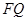 并延长交四边形
并延长交四边形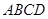 的一边于点
的一边于点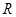 ,且满足
,且满足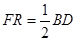 ,则
,则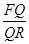 的值为_____________.
的值为_____________.