题目内容
【题目】(本题满分10分)
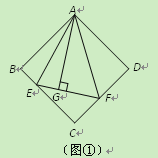
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求![]() 的度数.
的度数.
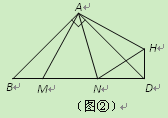
(2)如图②,在Rt△ABD中,![]() ,
,![]() ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且![]() ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转![]() 至△ADH位置,连接
至△ADH位置,连接![]() ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若![]() ,
,![]() ,
,![]() ,求AG,MN的长.
,求AG,MN的长.
【答案】(1)在Rt△ABE和Rt△AGE中,![]() ,
,![]() ,
,
∴△ABE≌△AGE. ∴![]() .············································1分
.············································1分
同理,![]() .
.
∴![]() .·····························································2分
.·····························································2分
(2)![]() .··························································3分
.··························································3分
∵![]() ,
,![]() ,
,
∴![]() . ∴
. ∴![]() .
.
又∵![]() ,
,![]() ,
,
∴△AMN≌△AHN. ∴![]() .············································5分
.············································5分
∵![]() ,
,![]() ,
,
∴![]() . ∴
. ∴![]() .
.
∴![]() . ∴
. ∴![]() .·····················································6分
.·····················································6分
(3)由(1)知,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
解这个方程,得![]() ,
,![]() (舍去负根).
(舍去负根).
∴![]() .·····························································8分
.·····························································8分
∴![]() .
.
在(2)中,![]() ,
,![]() ,
,
∴![]() .·····························································9分
.·····························································9分
设![]() ,则
,则![]() .
.
∴![]() .即
.即![]() .·························································10分
.·························································10分
【解析】略

【题目】某工厂以每千克200元的价格购进甲种原料360千克,用于生产A、B两种产品,生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表:
产品/原料 | A | B |
甲(千克) | 9 | 4 |
乙(千克) | 3 | 10 |
乙种原料的价格为每千克300元,A产品每件售价3000元,B产品每件售价4200元,现将甲种原料全部用完,设生产A产品x件,B产品m件,公司获得的总利润为y元.
(1)写出m与x的关系式;
(2)求y与x的关系式;
(3)若使用乙种原料不超过510千克,生产A种产品多少件时,公司获利最大?最大利润为多少?


