题目内容
已知二次函数y=ax2+bx+c.(1)若a=1,b=-3,且二次函数的图象经过点(-2,15),求c的值;
(2)若a+c=1,b=2,且二次函数图象与y轴的交点在直线y=1与y=2之间,试说明这个二次函数图象的对称轴在直线x=1的右侧;
(3)若a+b+c=0,a>b>c,且二次函数的图象经过点(m,-a),与x轴交于A、B两点.请确定线段AB长的取值范围,并证明你的结论.
分析:(1)由于a=1,b=-3,且二次函数的图象经过点(-2,15),代入y=ax2+bx+c中即可得到关于c的方程,解方程即可求解;
(2)由a+c=1得到a=1-c,而对称轴为直线x=-
,又b=2,代入其中得到x=-
,而二次函数图象与y轴的交点在直线y=1与y=2之间,由此得到1<c<2,利用这个结论即可解决问题;
(3)设A(x1,0),B(x2,0)(x1<x2),则x1、x2是方程ax2+bx+c=0的两根,由求根公式得出x1、x2,根据AB=|x2-x1|求出线段AB长度的最小值
(2)由a+c=1得到a=1-c,而对称轴为直线x=-
| b |
| 2a |
| 2 |
| 1-c |
(3)设A(x1,0),B(x2,0)(x1<x2),则x1、x2是方程ax2+bx+c=0的两根,由求根公式得出x1、x2,根据AB=|x2-x1|求出线段AB长度的最小值
解答:解:(1)当a=1,b=-3时,二次函数为y=x2-3x+c,
因为该函数的图象经过点(-2,15),
所以15=(-2)2-3×(-2)+c,
解得c=5;
(2)∵由题意1<c<2,
∴0<c-1<1,
∴
>1,
由二次函数知其对称轴x= -
,
由b=2,a=1-c,则x=
,
∴二次函数知其对称轴大于1;
(3)因为二次函数y=ax2+bx+c的图象经过点(m,-a),
所以am2+bm+c+a=0,
所以q为方程am2+bm+c+a=0的根,
于是,△=b2-4a(a+c)≥0,
又a+b+c=0,所以△=b(3a-c)≥0,
又a>b>c,知a>0,c<0,
所以3a-c>0,
所以b≥0.
设x1=
,x2=
,
则AB之间的距离=
=
=
=1-
>1.
即线段AB的长>1.
因为该函数的图象经过点(-2,15),
所以15=(-2)2-3×(-2)+c,
解得c=5;
(2)∵由题意1<c<2,
∴0<c-1<1,
∴
| 1 |
| c-1 |
由二次函数知其对称轴x= -
| b |
| 2a |
由b=2,a=1-c,则x=
| 1 |
| c-1 |
∴二次函数知其对称轴大于1;
(3)因为二次函数y=ax2+bx+c的图象经过点(m,-a),
所以am2+bm+c+a=0,
所以q为方程am2+bm+c+a=0的根,
于是,△=b2-4a(a+c)≥0,
又a+b+c=0,所以△=b(3a-c)≥0,
又a>b>c,知a>0,c<0,
所以3a-c>0,
所以b≥0.
设x1=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
则AB之间的距离=
2
| ||
| 2a |
| ||
| a |
| a-c |
| a |
| c |
| a |
即线段AB的长>1.
点评:本题考查的是二次函数的综合题型,其中涉及的知识点有抛物线的平移、抛物线交点坐标与其解析式的组成的方程组的解的关系及等腰三角形的性质与判定,也利用了三角函数的定义,综合性比较强,定义学生的能力要求比较高,平时加强训练.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
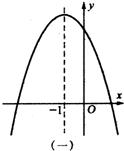 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
