题目内容
【题目】如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
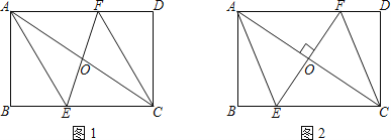
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
【答案】(1)见解析;(2)EF=![]() .
.
【解析】
(1)证明△AOF≌△COE全等,可得AF=EC,∵AF∥EC,∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,且EF⊥AC,∴四边形AECF为菱形,假设BE=a,根据勾股定理求出a,从而得知EF的长度;
解:(1)∵矩形ABCD,∴AF∥EC,AO=CO
∴∠FAO=∠ECO
∴在△AOF和△COE中,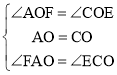 ,
,
∴△AOF≌△COE(ASA)
∴AF=EC
又∵AF∥EC
∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
设BE=a,则AE=EC=3-a
∴a2+22=(3-a)2
∴a=![]()
则AE=EC=![]() ,
,
∵AB=2,BC=3,
∴AC=![]() =
=![]()
∴AO=OC=![]() ,
,
∴OE=![]() =
=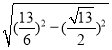 =
=![]() ,
,
∴EF=2OF=![]() .
.

练习册系列答案
相关题目