Question

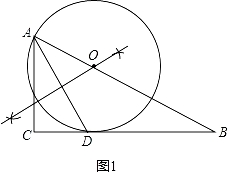
【题目】已知，如图，在Rt△ABC中，∠C=90，∠BAC的角平分线AD交BC边于D．

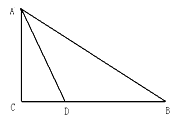
（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；

（2）AB=6，BD=，求（1）中⊙O的半径

Answer 1

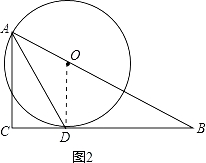
【答案】（1）如图（2）⊙O的半径为2．

【解析】

试题分析：（1）根据题意得：O点应该是AD垂直平分线与AB的交点；由的角平分线AD交BC边于D，与圆的性质可证得，又由，则问题得证；

（2）设的半径为r ，则在中，利用勾股定理列出关于r的方程，通过解方程即可求得r的值；

试题解析：

（1）如图1，作AD的垂直平分线交AB于点O，O为圆心，OA为半径作圆．

判断结果：BC是⊙O的切线．

如图2，连接OD．

∵AD平分，

∴

∵OA=OD，

∴

∴，

∴，

∴，

∵，

∴，

即：，

∵OD是⊙O的半径，

∴BC是⊙O的切线．

（2）设⊙O的半径为r，则OB=6﹣r，

∵，

在中，，

即，

解得r=2．

故⊙O的半径是2．