题目内容
【题目】如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.下列结论:①△ABE≌△ADF;②CE=CF;③∠AEB=75°;④BE+DF=EF;⑤S△ABE+S△ADF=S△CEF , 其中正确的是①②③⑤(只填写序号). 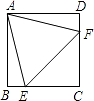
【答案】①②③⑤
【解析】解:∵AB=AD,AE=AF=EF, ∴△ABE≌△ADF(HL),△AEF为等边三角形,
∴BE=DF,又BC=CD,
∴CE=CF,
∴∠BAE= ![]() (∠BAD﹣∠EAF)=
(∠BAD﹣∠EAF)= ![]() (90°﹣60°)=15°,
(90°﹣60°)=15°,
∴∠AEB=90°﹣∠BAE=75°,
∴①②③正确,
在AD上取一点G,连接FG,使AG=GF,
则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG= ![]() ,
,
∴AD=CD=2+ ![]() ,CF=CE=CD﹣DF=1+
,CF=CE=CD﹣DF=1+ ![]() ,
,
∴EF= ![]() CF=
CF= ![]() +
+ ![]() ,而BE+DF=2,
,而BE+DF=2,
∴④错误,
⑤∵S△ABE+S△ADF=2× ![]() AD×DF=2+
AD×DF=2+ ![]() ,
,
S△CEF= ![]() CE×CF=
CE×CF= ![]() =2+
=2+ ![]() ,
,
∴⑤正确.
所以答案是:①②③⑤.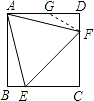
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】肇庆市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如下表:
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
则该周PM2.5指数的众数和中位数分别是( )
A. 150,150B. 150,155C. 155,150D. 150,152.5