题目内容
设m是不小于-1的实数,关于x的方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1、x2,(1)若x12+x22=6,求m值;
(2)求
 的最大值.
的最大值.
【答案】分析:(1)首先根据根的判别式求出m的取值范围,利用根与系数的关系,求出符合条件的m的值.
(2)把利用根与系数的关系得到的关系式代入代数式,细心化简,结合m的取值范围求出代数式的最大值.
解答:解:∵方程有两个不相等的实数根,
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x12+x22=(x1+x2)2-2x1x2=4(m-2)2-2(m2-3m+3)=2m2-10m+10=6
∴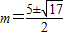 ,
,
∵-1≤m<1,
∴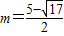 ;
;
(2)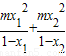 =
=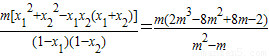
=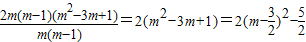 (-1≤m<1).
(-1≤m<1).
∴当m=-1时,式子取最大值为10.
点评:本题的计算量比较大,需要很细心的求解.用到一元二次方程的根的判别式△=b2-4ac来求出m的取值范围;利用根与系数的关系x1+x2=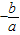 ,x1x2=
,x1x2= 来化简代数式的值.
来化简代数式的值.
(2)把利用根与系数的关系得到的关系式代入代数式,细心化简,结合m的取值范围求出代数式的最大值.
解答:解:∵方程有两个不相等的实数根,
∴△=b2-4ac=4(m-2)2-4(m2-3m+3)=-4m+4>0,
∴m<1,
结合题意知:-1≤m<1.
(1)∵x12+x22=(x1+x2)2-2x1x2=4(m-2)2-2(m2-3m+3)=2m2-10m+10=6
∴
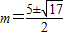 ,
,∵-1≤m<1,
∴
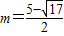 ;
;(2)
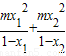 =
=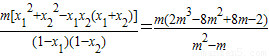
=
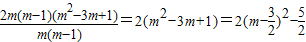 (-1≤m<1).
(-1≤m<1).∴当m=-1时,式子取最大值为10.
点评:本题的计算量比较大,需要很细心的求解.用到一元二次方程的根的判别式△=b2-4ac来求出m的取值范围;利用根与系数的关系x1+x2=
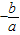 ,x1x2=
,x1x2= 来化简代数式的值.
来化简代数式的值. 
练习册系列答案
相关题目
 ,顶点为C,设m是不小于-1的实数.
,顶点为C,设m是不小于-1的实数. 的最大值.
的最大值.