题目内容
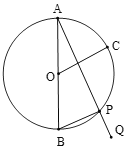
【题目】如图,AB为⊙O的直径,AB=3,弧AC的度数是![]() ,P为弧BC上一动点,延长AP到点Q,使
,P为弧BC上一动点,延长AP到点Q,使![]() .若点P由B运动到C,则点Q运动的路径长为______.
.若点P由B运动到C,则点Q运动的路径长为______.
【答案】![]()
【解析】
连接BQ,如图,根据圆周角定理得到∠APB=90°,再证明△ABP∽△AQB得到∠ABQ=∠APB=90°,则可判定BQ为⊙O的切线,点Q运动的路径长为切线长,然后计算P点在C点时BQ的长即可.
解:连接BQ,如图,
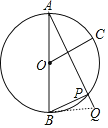
∵AB为⊙O的直径,
∴∠APB=90°,
∵APAQ=AB2
即![]()
而∠BAP=∠QAB,
∴△ABP∽△AQB,
∴∠ABQ=∠APB=90°,
∴BQ为⊙O的切线,点Q运动的路径长为切线长,
∵弧AC的度数是60°,
∴∠AOC=60°,
∴∠OAC=60°,
当点P在C点时,∠BAQ=60°,
∴BQ=![]() AB=3
AB=3![]() ,
,
即点P由B运动到C,则点Q运动的路径长为3![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目
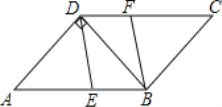
【题目】如图,在△ABC中,D、E分别是AC、AB的中点,CF∥AB交ED的延长线于点F,连接AF、CE.
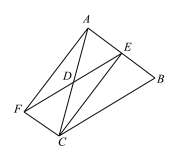
(1)求证:四边形BCEF是平行四边形;
(2)当△ABC满足什么条件时,四边形AECF是菱形.
【题目】知抛物线y=x2﹣4x+2.
(1)此抛物线与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
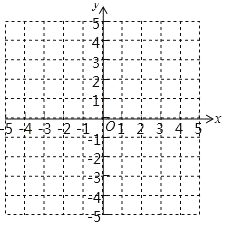
(3)结合图象回答:若点A(6,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是 .