题目内容
含30°角的直角三角板ABC中,∠A=30°,将其绕直角顶点C顺时针旋转α角(0°<α<120°且α≠90°),得到Rt△A'B'C,A'C边与AB所在直线交于点D,过点 D作DE∥A'B'交CB'边于点E,连接BE。
(1)如图1,当A'B'边经过点B时,α=_____°;
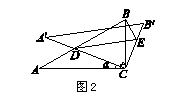
(2)如图2,在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
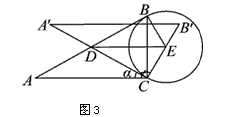
(3)如图2,设BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=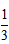 S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。
S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。
(1)如图1,当A'B'边经过点B时,α=_____°;
(2)如图2,在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
(3)如图2,设BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=
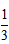 S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。
S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。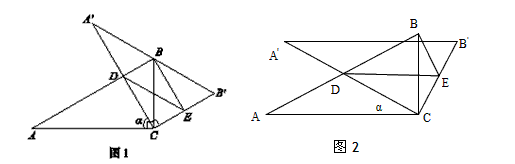
| 解:(1)当A′B′边经过点B时,α=60°; (2)猜想:如图2,点D在AB边上时,m=2; 证明:当 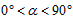 时,点D在AB边上(如图2), 时,点D在AB边上(如图2),∵ DE∥A′B′, ∴ 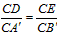 , ,由旋转性质可知,CA=CA′,CB=CB′,∠ACD=∠BCE, ∴ 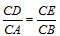 , ,∴△CAD∽△CBE, ∴∠A =∠CBE=30°, ∵ 点D在AB边上,∠CBD=60°, ∴ 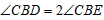 , ,即m=2; (3)在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1, ∴AB=2,  , ,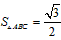 由△CAD∽△CBE 得, 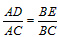 ∵AD=x, ∴ 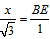 , ,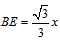 当点D在AB边上时,AD=x, 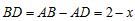 ,∠DBE=90°, ,∠DBE=90°,此时, 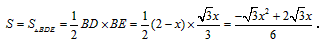 , ,当S= 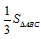 时, 时,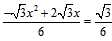 , ,整理,得 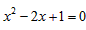 , ,解得 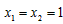 ,即AD=1, ,即AD=1,此时D为AB中点,故∠DCB=60°,∠BCE=30°=∠CBE, ∴EC=EB, ∵ 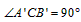 , ,点E在CB′边上, ∴圆心E到A′C的距离EC等于⊙E的半径EB, ∴直线A′C与⊙E相切。 |
  |

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:
14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形: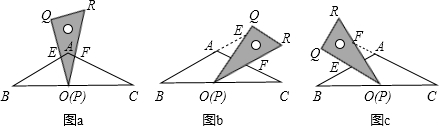
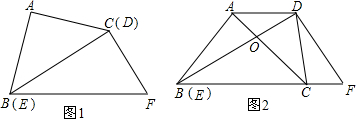

 如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(
如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(