题目内容
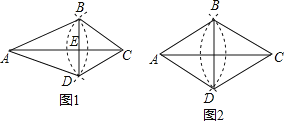
【题目】将纸片△ABC沿DE折叠使点A落在A'处的位置.
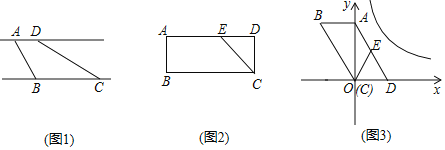
(1)如果A'落在四边形BCDE的内部(如图1),∠A'与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A'落在四边形BCDE的外部(如图2),这时∠A'与∠1、∠2之间又存在怎样的数量关系?并说明理由.
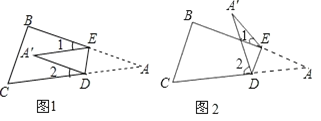
【答案】(1)2∠A'=∠1+∠2,理由见解析;(2)2∠A'=∠2﹣∠1,理由见解析.
【解析】
(1)由折叠的性质可得:∠AED=∠A'ED,∠ADE=∠A'DE,然后根据平角的定义可得∠1、∠2与∠AED、∠ADE的关系,再相加并利用三角形的内角和整理化简即得结论;
(2)如图3,由折叠的性质可得∠A=∠A',然后利用三角形的外角性质可得∠DME=∠A'+∠1,∠2=∠A+∠DME,进一步即可得出结论.
解:(1)2∠A'=∠1+∠2,
理由:∵将纸片△ABC沿DE折叠使点A落在A'处的位置,∴∠AED=∠A'ED,∠ADE=∠A'DE.
∵∠AED+∠ADE=180°﹣∠A,∠1=180°-∠AED-∠A'ED=180°-2∠AED,∠2=180°﹣∠ADE-∠A'DE=180°-2∠ADE,
∴∠1+∠2=180°+180°﹣2(∠AED+∠ADE)=360°﹣2(180°﹣∠A')=2∠A';
∴2∠A'=∠1+∠2;
(2)2∠A'=∠2﹣∠1,
理由:如图3,∵将纸片△ABC沿DE折叠使点A落在A'处的位置,∴∠A=∠A'.
∵∠DME=∠A'+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A'+∠1,即2∠A'=∠2﹣∠1.

 津桥教育计算小状元系列答案
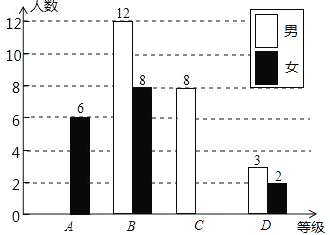
津桥教育计算小状元系列答案【题目】)6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
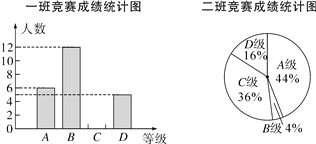
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.